Cách 1: Dùng hình học thuần túy:
Dựng các điểm như hình vẽ
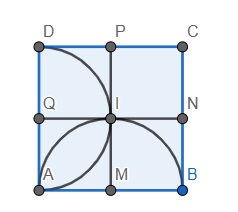
Khi đó diện tích phần màu xanh lá chính bằng tổng diện tích của hình vuông CNIP và hai lần diện tích của hình giới hạn bởi PD, PI và cung tròn DI.
Khi đó \(x=S_{CNIP}+2\left(S_{DQIP}-S_{QDI}\right)=\left(\dfrac{1}{2}\right)^2+2\left(\left(\dfrac{1}{2}\right)^2-\dfrac{1}{4}\pi\left(\dfrac{1}{2}\right)^2\right)=\dfrac{1}{4}+2\left(\dfrac{1}{4}-\dfrac{\pi}{16}\right)=\dfrac{6-\pi}{8}\)
Cách 2: Dùng tích phân
Xét hệ trục Oxy như hình vẽ
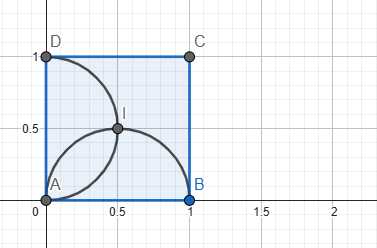
Khi đó phương trình đường tròn đường kính DA tính từ 0 đến 0,5 là: \(x^2+\left(y-\dfrac{1}{2}\right)^2=\dfrac{1}{4}\Leftrightarrow y-\dfrac{1}{2}=\sqrt{\dfrac{1}{4}-x^2}\Leftrightarrow y=\dfrac{1}{2}+\sqrt{\dfrac{1}{4}-x^2}\)
Phương trình đường tròn đường kính AB là \(\left(x-\dfrac{1}{2}\right)^2+y^2=\dfrac{1}{4}\Leftrightarrow y=\sqrt{\dfrac{1}{4}-\left(x-\dfrac{1}{2}\right)^2}=\sqrt{x-x^2}\)
Do đó diện tích hình màu xanh lá là:
\(S=1-\left(S_{DIA}+S_{AIB}\right)=1-\left[\int\limits^{\dfrac{1}{2}}_0\left(\dfrac{1}{2}+\sqrt{\dfrac{1}{4}-x^2}-\sqrt{x-x^2}\right)dx+\dfrac{1}{2}\pi\left(\dfrac{1}{2}\right)^2\right]=1-\left(\dfrac{1}{4}+\dfrac{\pi}{18}\right)=\dfrac{6-\pi}{8}\)









