Bài tập cuối chương Dãy số, cấp số cộng, cấp số nhân SVIP

Tải ma trận In bài

Yêu cầu đăng nhập!

Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!

Câu 1 (1đ):

Cho dãy số $(u_n)$ xác định bởi $\left\{ \begin{aligned} & u_1=\dfrac{1}{2} \\ & u_n=\dfrac{1}{2-u_{n-1}},\,\forall n\ge 2 \\ \end{aligned} \right.$ . Khi đó $u_3$ có giá trị bằng

\dfrac{2}{3}

.

\dfrac{4}{3}

.

\dfrac{3}{2}

.

\dfrac{3}{4}

.

Câu 2 (1đ):

Cho dãy số $(u_n)$ xác định bởi $u_n=\dfrac{n-1}{n^2+2n+3}$ . Giá trị $u_{21}$ là

\dfrac{10}{243}

.

\dfrac{19}{443}

.

\dfrac{21}{443}

.

\dfrac{11}{243}

.

Câu 3 (1đ):

Cho dãy số $(u_n )$ với $u_n=\sin \dfrac{\pi }{n}$ . Khi đó, dãy số $(u_n)$

tăng.

bị chặn.

không bị chặn.

giảm.

Câu 4 (1đ):

Cho dãy số $(u_n)$ có $u_n=-n^2+n+1$ . Số $-19$ là số hạng thứ mấy của dãy số đã cho?

7

.

5

.

6

.

4

.

Câu 5 (1đ):

Cho cấp số cộng $(u_n)$ có $u_2=8, \, u_5=17$ . Công sai $d$ bằng

5

.

-5

.

-3

.

3

.

Câu 6 (1đ):

Cho cấp số cộng $(u_n)$ với $u_1=1$ ; công sai $d=2$ . Số hạng thứ ba của cấp số cộng đã cho là

u_3=5

.

u_3=7

.

u_3=4

.

u_3=3

.

Câu 7 (1đ):

Dãy số nào sau đây là cấp số cộng?

Dãy số

(b_n)

, với

b_n=\dfrac{1}{2^n-1},\,\forall n\in \mathbb{N}^*

.

Dãy số

(a_n)

, với

a_n=3n-2,\,\forall n \in \mathbb{N}^*

.

Dãy số

(c_n)

, với

c_n=2.3^n, \, \forall n\in \mathbb{N}^*

.

Dãy số

(d_n)

, với

d_n=2+5^n, \, \forall n\in \mathbb{N}^*

.

Câu 8 (1đ):

Cho cấp số cộng $(u_n)$ có số hạng đầu $u_1=3$ , công sai $d=-2$ thì số hạng thứ $5$ là

u_5=-5

.

u_5=-7

.

u_5=1

.

u_5=8

.

Câu 9 (1đ):

Câu 10 (1đ):

Câu 11 (1đ):

Câu 12 (1đ):

Câu 13 (1đ):

Cho dãy số $(u_n )$ có số hạng tổng quát $u_n=\sqrt{n+1}-\sqrt{n}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\dfrac{u_{n+1}}{u_n}=\dfrac{\sqrt{n+2}+\sqrt{n}}{\sqrt{n+3}+\sqrt{n+2}}$ .
b) $\dfrac{u_{2 \, 024}}{u_{2 \, 023}}<1$ .
c) $u_{n+1}<u_n, \, \forall n \in \mathbb{N}^*$ .
d) Dãy số $(u_n )$ là dãy số giảm.

Câu 14 (1đ):

Cho dãy số $(u_n)$ có số hạng tổng quát $u_n=\dfrac{n}{4^n}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Ta có $u_n=\dfrac{n}{4^n}<0, \, \forall n \in \mathbb{N}^*$ .
b) Ta có $\dfrac{u_{n+1}}{u_n}<1, \, \forall n\ge 1$ .
c) Ta có $u_{2 \, 024}<u_{2 \, 023}$ .
d) Dãy số $(u_n)$ là dãy số tăng.

Câu 15 (1đ):

Cho cấp số cộng $(u_n)$ có $u_1=123$ , $u_3-u_{15}=84$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số hạng thứ $17$ của cấp số cộng là $u_{17}=11.$
b) Công sai của cấp số cộng là $d=-7.$
c) Số hạng thứ $2$ của cấp số cộng là $u_2=130$ .
d) Tổng $17$ số hạng đầu tiên của cấp số cộng là $S_{17}=1\, 130$ .

Câu 16 (1đ):

Người ta trồng $3 \, 240$ cây theo một hình tam giác như sau: hàng thứ nhất trồng $1$ cây, hàng thứ hai trồng $2$ cây, hàng thứ ba trồng $3$ cây, …

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số cây mỗi hàng lập thành một cấp số cộng $(u_n)$ có số hạng đầu là $u_1=1$ .
b) Số cây mỗi hàng lập thành một cấp số cộng $(u_n)$ có công sai là $d=2$ .
c) Có tất cả $80$ hàng cây.
d) Hàng thứ $20$ trồng được $40$ cây.

Câu 17 (1đ):

Trong một hồ sen, số lá sen ngày hôm sau bằng $3$ lần số lá sen ngày hôm trước. Biết rằng ngày đầu có $1$ lá sen thì tới ngày thứ $10$ hồ sẽ đầy lá sen.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Nếu ngày đầu có $9$ lá sen thì tới ngày thứ $8$ hồ sẽ đầy lá sen.
b) Số lá sen lập thành cấp số nhân $(u_n)$ với $u_1=1$ và công bội $q=3$ .
c) Số lá sen lập thành cấp số cộng $(u_n)$ với $u_1=1$ và công bội $q=3$ .
d) Nếu ngày đầu có $9$ lá sen thì tới ngày thứ $9$ hồ sẽ đầy lá sen.

Câu 18 (1đ):

Cho dãy số $(u_n )$ biết $\left\{ \begin{aligned}&u_1=1; \, u_2=2 \\&u_{n+2}=au_{n+1}+(1-a)u_n, \, \forall n \in \mathbb{N}^*\\ \end{aligned} \right.$ . Tìm giá trị nguyên nhỏ nhất của $a$ để dãy số $(u_n )$ tăng.

Trả lời:

Câu 19 (1đ):

Người ta trồng $3 \, 003$ cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng $1$ cây, hàng thứ hai trồng $2$ cây, hàng thứ ba trồng $3$ cây, …, cứ tiếp tục trồng như thế cho đến khi hết số cây. Số hàng cây được trồng là bao nhiêu?

Trả lời:

Câu 20 (1đ):

Nguời ta thiết kế một cái tháp gồm $10$ tầng theo cách: Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích bề mặt trên của tầng ngay bên dưới và diện tích bề mặt của tầng $1$ bằng nửa diện tích bề mặt đế tháp. Biết diện tích bề mặt đế tháp là $12 \, 288$ m $^2$ , tính diện tích bề mặt trên cùng của tháp (đơn vị mét vuông).

Trả lời:

Câu 21 (1đ):

Cho hình vuông $(C_1)$ có cạnh bằng $a$ . Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông $(C_2)$ .

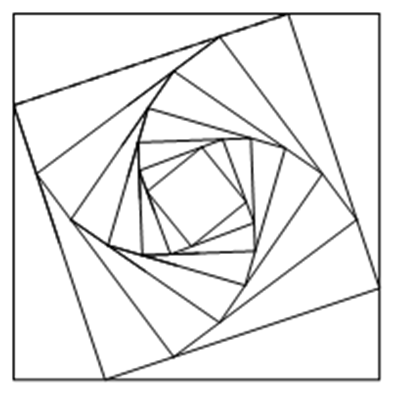
Từ hình vuông $(C_2)$ lại tiếp tục làm như trên ta nhận được dãy các hình vuông $C_1$ , $C_2$ , $C_3$ ,..., $C_n$ . Gọi $S_i$ là diện tích của hình vuông $C_i, \, (i \in \left\{ 1;2;3,..... \right\})$ . Đặt $T=S_1+S_2+S_3+...+S_n+...$ . Biết $T=\dfrac{32}{3}$ , tính $a$ ?

Trả lời:

OLM \copyright 2022