Đề ôn tập và kiểm tra giữa học kì I toán 11 cấu trúc mới mới nhất

Câu 1 (1đ):

Một đường tròn có đường kính là $50$ cm. Độ dài của cung tròn trên đường tròn có số đo là $\dfrac{\pi }{4}$ (làm tròn đến hàng đơn vị) bằng

40

cm.

20

cm.

19

cm.

36

cm.

Câu 2 (1đ):

Cho hình bình hành $ABCD$ và $S$ là điểm không thuộc mặt phẳng của hình bình hành. Giao tuyến của $(SAD)$ và $(SBC )$ là

SO

với

O

là giao điểm của

AC

và

BD

.

SI

với

I

là giao điểm của

AD

và

BC

.

Đường thẳng qua

S

và song song với

AB

.

Đường thẳng qua

S

và song song với

AD

.

Câu 3 (1đ):

Cho dãy số có các số hạng đầu là $\dfrac13; \, \dfrac{1}{3^2}; \, \dfrac{1}{3^3}; \, \dfrac{1}{3^4};...$ . Số hạng tổng quát của dãy số này là

\dfrac{1}{3^{n-1}}

\dfrac{1}{3^{n}}

.

\dfrac{1}{3^{n+1}}

.

\dfrac{1}{3^{n+2}}

.

Câu 4 (1đ):

Câu 5 (1đ):

Cho cấp số cộng $(u_n)$ với $u_1=1$ và $u_{100}=496$ . Công sai của cấp số cộng đã cho bằng

-5

.

\dfrac{99}{20}

.

5

.

6

.

Câu 6 (1đ):

Cho dãy số $(u_n )$ với $u_n=\sin \dfrac{\pi }{n}$ . Khi đó, dãy số $(u_n)$

tăng.

bị chặn.

không bị chặn.

giảm.

Câu 7 (1đ):

Phương trình $\cot x=3$ có nghiệm là

x=arc\cot 3+k\pi, \, k\in \mathbb{Z}

.

x=arc\cot 3+k2\pi, \, k\in \mathbb{Z}

.

x=\cot 3+k2\pi, \, k\in \mathbb{Z}

.

x=\cot 3+k\pi, \, k\in \mathbb{Z}

.

Câu 8 (1đ):

Hai hàm số nào sau đây tăng trên khoảng $\Big(0;\dfrac{\pi }{2} \Big)$ ?

y=\tan x

và

y=\cot x

.

y=\cot x

và

y=\sin x

.

y=\sin x

và

y=\tan x

.

y=\sin x

và

y=\cos x

.

Câu 9 (1đ):

Tập giá trị của hàm số $y=\sin 2x$ là

\left[ -1;1 \right]

.

\left[ 0;2 \right]

.

\left[ -2;2 \right]

.

\mathbb{R}

.

Câu 10 (1đ):

Cho tứ diện $ABCD$ . Gọi $I,\, J$ là các điểm lần lượt nằm trên các cạnh $AB,\, AD$ với $AI=\dfrac{1}{2}IB$ và $AJ=\dfrac{3}{2}JD$ . Giao điểm của đường thẳng $IJ$ với mặt phẳng $(BCD )$ là

Điểm

K

với

K = IJ \cap BD

.

Điểm

D

.

Điểm

I

.

Điểm

M

với

M = IJ \cap CD

.

Câu 11 (1đ):

Cho cấp số cộng $(u_n)$ thoả mãn $\left\{ \begin{aligned} u_2-u_3+u_5=10 \\ u_4+u_6=26\\ \end{aligned} \right.$ . Giá trị $S=u_1+u_5+u_9+...+u_{2 \, 021}$ bằng

1 \, 533 \, 686

.

6 \, 730 \, 444

.

2 \, 023 \, 563

.

6 \, 734 \, 134

.

Câu 12 (1đ):

Số điểm biểu diễn nghiệm của phương trình $\tan 2x=1$ trên đường tròn lượng giác là

8

.

2

.

6

.

4

.

Câu 13 (1đ):

Cho hình chóp $S.ABCD$ , gọi hai điểm $M,\,N$ lần lượt là trung điểm $SD,\,CD$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $CD$ là giao tuyến của hai mặt phẳng $(SCD )$ và $(ABCD )$ .
b) Gọi $O$ là giao điểm của $AC$ và $BD$ . $SO$ là giao tuyến của hai mặt phẳng $(SAC )$ và $(SBD )$ .
c) Giả sử $AB$ không song song $CD.$ Gọi $P$ là giao điểm của $AC$ và $BN.$ $SP$ là giao tuyến của hai mặt phẳng $(SAB )$ và $(SCD )$ .
d) Giao điểm của $SA$ và mặt phẳng $(BMN )$ là giao điểm của $SA$ và $BN.$

Câu 14 (1đ):

Cho phương trình lượng giác $\sin \Big(3x+\dfrac{\pi }{3} \Big)=-\dfrac{\sqrt{3}}{2}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Phương trình có nghiệm $\left[ \begin{aligned} &x=-\dfrac{\pi }{9}+k\dfrac{2\pi }{3} \\ &x=\dfrac{\pi }{3}+k\dfrac{2\pi }{3} \\ \end{aligned}, \, (k\in \mathbb{Z}) \right.$ .
b) Phương trình có nghiệm âm lớn nhất bằng $-\dfrac{2\pi }{9}$ .
c) Trên khoảng $\Big(0;\dfrac{\pi }2\Big)$ phương trình đã cho có $3$ nghiệm.
d) Tổng các nghiệm của phương trình trong khoảng $\left(0;\dfrac{\pi }{2} \right)$ bằng $\dfrac{7\pi }{9}$ .

Câu 15 (1đ):

Tương truyền rằng nhà vua Ấn Độ cho phép người phát minh ra bàn cờ vua được lựa chọn phần thưởng tùy theo sở thích. Người đó xin nhà vua: "Bàn cờ có $64$ ô, với ô thứ nhất thần xin nhận $1$ hạt thóc, ô thứ hai thì gấp đôi ô đầu, ô thứ ba thì lại gấp đôi ô thứ hai, … cứ như vậy ô sau nhận số hạt thóc gấp đôi phần thưởng dành cho ô liền trước và thần xin nhận tổng số các hạt thóc ở $64$ ô". Biết rằng khối lượng của $100$ hạt thóc là $20$ gam.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số hạt thóc ở $64$ ô là một cấp số nhân có $u_1=1;\,q=2$ .
b) Số hạt thóc ở ô thứ tám là $2^8$ .
c) Tổng khối lượng thóc của $64$ ô trên bàn cờ là $364$ tỉ tấn.
d) Giả sử người đó muốn chở số thóc ở trên $32$ ô đầu tiên về bằng tàu thủy, biết rằng mỗi chuyến tàu chở tối đa $10$ tấn hàng hóa. Khi đó, người đó cần tối thiểu $85$ chuyến tàu để chở hết số thóc đó.

Câu 16 (1đ):

Cho hàm số $f(x)=\tan 2x-1$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Giá trị của hàm số tại $x=\dfrac{\pi }{8}$ bằng $0$ .
b) Giá trị của hàm số tại $x=\dfrac{\pi }{3}$ bằng $-\sqrt{3}-1$ .
c) Có 3 giá trị $x$ thuộc $[0;\pi ]$ khi hàm số đạt giá trị bằng $-2$ .
d) Hàm số đã cho là hàm tuần hoàn.

Câu 17 (1đ):

Trong thời gian liên tục $25$ năm, một người lao động luôn gửi đúng $4 \, 000 \, 000$ đồng vào một ngày cố định của tháng ở ngân hàng $M$ với lãi suất không thay đổi trong suốt thời gian gửi tiền là $0,6\%$ tháng. Gọi $A$ đồng là số tiền người đó có được sau $25$ năm. Tính $A$ , đơn vị triệu đồng, làm tròn tới hàng đơn vị.

Trả lời:

Câu 18 (1đ):

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $I,\,K$ lần lượt là trung điểm của $BC$ và $CD$ . Gọi $M$ là trung điểm của $SB$ . Gọi $F$ là giao điểm của $DM$ và $(SIK)$ . Tính tỉ số $\dfrac{MF}{MD}$ .

Trả lời:

Câu 19 (1đ):

Sinh nhật bạn của An vào ngày $1$ tháng năm. An muốn mua một món quà sinh nhật cho bạn thân của mình nên quyết định bỏ ống heo $1 \, 000$ đồng vào ngày $01$ tháng $01$ năm $2016$ , sau đó cứ liên tục ngày sau hơn ngày trước $1 \, 000$ đồng. Hỏi đến ngay trước ngày sinh nhật của bạn thân, An đã tích lũy được bao nhiêu tiền? (ghi kết quả dưới dạng số thập phân, đơn vị nghìn đồng)

Trả lời:

Câu 20 (1đ):

Trong môn cầu lông, khi phát cầu, người chơi cần đánh cầu qua khỏi lưới sang phía sân đối phương và không được để cho cầu rơi ngoài biên. Trong mặt phẳng toạ độ $Oxy$ , chọn điểm có tọa độ $\left(O;y_0\right)$ là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời khỏi mặt vợt là: $y=\dfrac{-g.x^2}{2.v_{0}^{2}.\cos^{2}\alpha}+\tan (\alpha).x+y_0$ ; trong đó: $g$ là gia tốc trọng trường (thường được chọn là $9,8$ m/s $^{2}$ ; $\alpha$ là góc phát cầu (so với phương ngang của mặt đất); ${{v}_{0}}$ là vận tốc ban đầu của cầu; ${{y}_{0}}$ là khoảng cách từ vị trí phát cầu đến mặt đất. Quỹ đạo chuyển động của quả cầu lông là một parabol như hình vẽ.

loading...

Một người chơi cầu lông đang đứng khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa) là $6,68$ m. Người chơi đó đã phát cầu với góc tối đa khoảng bao nhiêu độ so với mặt đất? (biết cầu rời mặt vợt ở độ cao $0,7$ m so với mặt đất và vận tốc xuất phát của cầu là $8$ m/s, bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng thẳng đứng, làm tròn kết quả tới hàng đơn vị).

Trả lời:

Câu 21 (1đ):

Một chiếc đu quay có bán kính $75$ m, tâm của vòng quay ở độ cao $90$ m, thời gian thực hiện mỗi vòng quay của đu quay là $30$ phút.

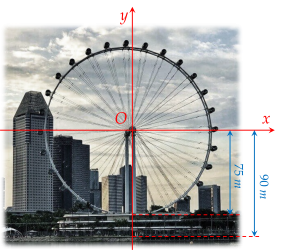
loading...

Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau $20$ phút quay, người đó ở độ cao bao nhiêu mét? (làm tròn kết quả tới hàng phần mười)

Trả lời:

Câu 22 (1đ):

Gọi $n$ là số nghiệm của phương trình $\sin \left(2x+{{30}^\circ} \right)=\dfrac{\sqrt{3}}{2}$ trên khoảng $\left(-{{180}^\circ};{{180}^\circ} \right)$ . Tìm $n$ .

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP