Đề ôn tập và kiểm tra giữa học kì I toán 11 cấu trúc mới mới nhất

Câu 1 (1đ):

Góc có số đo $60^\circ$ đổi sang rađian là

\dfrac{\pi}{5}

.

\dfrac{\pi }{4}

.

\dfrac{\pi}3

.

\dfrac{3\pi }{2}

.

Câu 2 (1đ):

Cho hình bình hành $ABCD$ và $S$ là điểm không thuộc mặt phẳng của hình bình hành. Giao tuyến của $(SAD)$ và $(SBC )$ là

SO

với

O

là giao điểm của

AC

và

BD

.

SI

với

I

là giao điểm của

AD

và

BC

.

Đường thẳng qua

S

và song song với

AB

.

Đường thẳng qua

S

và song song với

AD

.

Câu 3 (1đ):

Cho dãy số có các số hạng đầu là $\dfrac13; \, \dfrac{1}{3^2}; \, \dfrac{1}{3^3}; \, \dfrac{1}{3^4};...$ . Số hạng tổng quát của dãy số này là

\dfrac{1}{3^{n-1}}

\dfrac{1}{3^{n}}

.

\dfrac{1}{3^{n+1}}

.

\dfrac{1}{3^{n+2}}

.

Câu 4 (1đ):

Câu 5 (1đ):

Một cấp số cộng $(u_n)$ , có $u_1=\dfrac12;\,u_{12}=\dfrac72$ . Công sai $d$ của cấp số cộng đó là

d=\dfrac{11}{3}

.

d=\dfrac{10}{3}

.

d=\dfrac{3}{11}

.

d=\dfrac{3}{10}

.

Câu 6 (1đ):

Cho dãy số $(u_n )$ với $u_n=\sin \dfrac{\pi }{n}$ . Khi đó, dãy số $(u_n)$

tăng.

bị chặn.

không bị chặn.

giảm.

Câu 7 (1đ):

Phương trình $\cot x=\cot \alpha$ có nghiệm là

x=k2\pi

,

k\in \mathbb{Z}

.

x=k\pi

,

k\in \mathbb{Z}

.

x=\alpha +k2\pi

,

k\in \mathbb{Z}

.

x=\alpha +k\pi, \, k\in \mathbb{Z}

.

Câu 8 (1đ):

Hai hàm số nào sau đây tăng trên khoảng $\Big(0;\dfrac{\pi }{2} \Big)$ ?

y=\tan x

và

y=\cot x

.

y=\cot x

và

y=\sin x

.

y=\sin x

và

y=\tan x

.

y=\sin x

và

y=\cos x

.

Câu 9 (1đ):

Giá trị lớn nhất của hàm số $y=3\sin x$ là

3

.

-3

.

2

.

1

.

Câu 10 (1đ):

Cho tứ diện $ABCD$ . Gọi $I,\, J$ là các điểm lần lượt nằm trên các cạnh $AB,\, AD$ với $AI=\dfrac{1}{2}IB$ và $AJ=\dfrac{3}{2}JD$ . Giao điểm của đường thẳng $IJ$ với mặt phẳng $(BCD )$ là

Điểm

K

với

K = IJ \cap BD

.

Điểm

D

.

Điểm

I

.

Điểm

M

với

M = IJ \cap CD

.

Câu 11 (1đ):

Một cấp số cộng có số hạng đầu $u_{1} = 2 \, 018$ công sai $d = -5$ . Bắt đầu từ số hạng nào của cấp số cộng đó thì nó nhận giá trị âm?

u_{403}

.

u_{406}

.

u_{405}

.

u_{404}

.

Câu 12 (1đ):

Số điểm biểu diễn nghiệm của phương trình $\tan 2x=1$ trên đường tròn lượng giác là

8

.

2

.

6

.

4

.

Câu 13 (1đ):

Cho hình chóp $S.ABCD$ , có đáy $ABCD$ là một hình bình hành tâm $O$ . Gọi $I,\,K$ lần lượt là trung điểm của $SB$ và $SD$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $SO$ là giao tuyến của $(SAC)$ và $(SBD)$ .
b) Giao điểm $J$ của $SA$ với $(CKB)$ thuộc đường thẳng đi qua $K$ và song song với $DC$ .
c) Giao tuyến của $(OIA)$ và $(SCD)$ là đường thẳng đi qua $C$ và song song với $SD$ .
d) $CD//IJ$ .

Câu 14 (1đ):

Cho phương trình $\sin \Big(2x-\dfrac{\pi }{4} \Big)=\sin \Big(x+\dfrac{3\pi }{4} \Big)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Phương trình có nghiệm $\left[ \begin{aligned} &x=\pi +k2\pi \\ &x=\dfrac{\pi }{6}+k\dfrac{2\pi }{3} \\ \end{aligned}, \,(k\in \mathbb{Z})\right.$ .
b) Trong khoảng $(0;\pi)$ phương trình có $2$ nghiệm.
c) Tổng các nghiệm của phương trình trong khoảng $(0;\pi)$ bằng $\dfrac{7\pi }{6}$ .
d) Trong khoảng $(0;\pi)$ phương trình có nghiệm lớn nhất bằng $\dfrac{5\pi }{6}$ .

Câu 15 (1đ):

Cho cấp số nhân $(u_n)$ biết rằng $u_1+u_2+u_3=168$ và $u_4+u_5+u_6=21$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số hạng $u_1=90$ .
b) Công bội của cấp số nhân bằng $2$ .
c) Số $24$ là số hạng thứ $3$ của cấp số nhân.
d) Tổng của $10$ số hạng đầu cấp số nhân đã cho bằng $\dfrac{3 \, 069}{16}$ .

Câu 16 (1đ):

Cho hàm số $f(x)=\tan x$ và $g(x)=\cot^2 x-\dfrac{\sin 2x}{2}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Tập xác định hàm số $f(x)$ là $D=\mathbb{R}\backslash \Big\{ \dfrac{\pi }{2}+k\pi \, \big\| \, k\in \mathbb{Z} \Big\}$ .
b) Hàm số $f(x)$ là hàm số không tuần hoàn.
c) Tập xác định hàm số $g(x)$ là $D=\mathbb{R}\backslash \{k\pi \, \big\| \, k\in \mathbb{Z}\}$ .
d) Hàm số $g(x)$ là hàm số tuần hoàn.

Câu 17 (1đ):

Trong thời gian liên tục $25$ năm, một người lao động luôn gửi đúng $4 \, 000 \, 000$ đồng vào một ngày cố định của tháng ở ngân hàng $M$ với lãi suất không thay đổi trong suốt thời gian gửi tiền là $0,6\%$ tháng. Gọi $A$ đồng là số tiền người đó có được sau $25$ năm. Tính $A$ , đơn vị triệu đồng, làm tròn tới hàng đơn vị.

Trả lời:

Câu 18 (1đ):

Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O$ , $M$ là một điểm thuộc đoạn $SA$ sao cho $2MA=SM$ , điểm $N$ là điểm thuộc tia đối của tia $OS$ sao cho $3ON=SO$ , $G$ là trọng tâm tam giác $SCD$ . Gọi $K=SD\cap (GMN )$ . Biết rằng $\dfrac{SK}{KD}=\dfrac{a}{b}(a,b\in \mathbb{N} )$ và $(a,b )=1$ . Tính $S=a+b$ .

Trả lời:

Câu 19 (1đ):

Ông Sơn trồng cây trên một mảnh đất hình tam giác theo quy luật: ở hàng thứ nhất có $1$ cây, hàng thứ hai có $2$ cây, hàng thứ ba có $3$ cây…, ở hàng thứ $n$ có $n$ cây. Biết rằng ông đã trồng hết $11 \, 325$ cây. Số hàng cây được trồng theo cách trên là bao nhiêu?

Trả lời:

Câu 20 (1đ):

Trong một thí nghiệm, một viên bi sắt được gắn vào một đầu lò xo đàn hồi, đầu còn lại được cố định vào một thanh treo ngang. Sau khi viên bi được kéo xuống và thả ra, nó bắt đầu di chuyển lên xuống. Khi đó, chiều cao $h$ cm của bi so với mặt đất theo thời gian $t$ giây được cho bởi công thức: $h=100-30\cos 20t.$ Tính thời điểm đầu tiên mà bi sắt đạt chiều cao cao nhất kể từ khi nó được thả ra (làm tròn kết quả đến hàng phần trăm).

Trả lời:

Câu 21 (1đ):

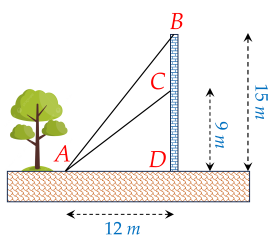
loading...

Từ một vị trí $A$ , người ta buộc hai sợi cáp $AB$ và $AC$ đến một cái trụ cao $15$ m, được dựng vuông góc với mặt đất, chân trụ ở vị trí $D$ . Biết $CD=9$ m và $AD=12$ m. Tìm góc nhọn $\alpha =\widehat{BAC}$ tạo bởi hai sợi dây cáp đó, đồng thời tính gần đúng $\alpha$ (làm tròn đến hàng phần mười, đơn vị độ).

Trả lời:

Câu 22 (1đ):

Gọi $n$ là số nghiệm của phương trình $\sin \left(2x+{{30}^\circ} \right)=\dfrac{\sqrt{3}}{2}$ trên khoảng $\left(-{{180}^\circ};{{180}^\circ} \right)$ . Tìm $n$ .

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP