Đề ôn tập và kiểm tra giữa học kì I toán 10 mới nhất

Câu 1 (1đ):

Câu 2 (1đ):

Trong các câu sau, có bao nhiêu câu là mệnh đề chứa biến?

a) Bạn học toán tốt không?

b) $128$ chia hết cho $4$ .

c) $5x-4>x^2$ .

d) $(2n+3)$ chia hết cho $4$ .

4.

2.

3.

1.

Câu 3 (1đ):

Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp $K=\Big\{ x \in \mathbb{R}\, \big| \, |x| \le 3 \Big\}$ ta có

K=\left[ -3;3 \right]

.

K=\left(-\infty ;-3 \right] \cup \left[ 3;+\infty \right)

.

K=\left[ 3;+\infty \right)

.

K=\left(-3;3 \right)

.

Câu 4 (1đ):

Hệ bất phương trình nào sau đây không là hệ bất phương trình bậc nhất hai ẩn?

\left\{ \begin{aligned} & x+y-6>0 \\ & x \ge 0 \\ & y\ge 0 \\ & 3x+y \le 6 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x<0 \\ & x+y \le \dfrac32 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & -2x + y > 3^2 \\ & x + 4^2y \le 1 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x \ge 1 \\ & 2x - xy\ge 0 \\ \end{aligned} \right.

.

Câu 5 (1đ):

Cho bất phương trình $-2x+\sqrt{3}y+\sqrt{2} \le 0$ có tập nghiệm là $S$ . Khẳng định nào sau đây đúng?

(1 ; 1) \in S

.

(4 ; 0) \notin S

.

(1;-3) \notin S

.

\Big(\dfrac{\sqrt{2}}{2};0 \Big) \in S

.

Câu 6 (1đ):

Cho hình chữ nhật $ABCD$ . Vectơ nào sau đây có độ dài lớn nhất?

\overrightarrow{BC}-\overrightarrow{BA}

.

\overrightarrow{0}

.

\overrightarrow{AD}

.

\overrightarrow{AB}

.

Câu 7 (1đ):

Giá trị của $B=\cos^2 73^\circ + \cos^2 87^\circ + \cos^2 3^\circ + \cos^2 17^\circ$ là

-2

.

2

.

1

.

\sqrt{2}

.

Câu 8 (1đ):

Cho tam giác $ABC$ có độ dài các cạnh là $a$ , $b$ và $c$ . Mệnh đề nào sau đây đúng?

a^2=b^2+c^2-2bc\cos B

.

a^2=b^2+c^2-2bc\cos A

.

a^2=b^2+c^2+2bc\cos A

.

a^2=b^2+c^2-2bc\cos C

.

Câu 9 (1đ):

Cho $A=\left(-\infty ;-2 \right]$ , $B=\left[ 3;+\infty \right)$ , $C=\left(0;4 \right).$ Khi đó tập $\left(A\cup B \right) \cap C$ là

\left(-\infty ;-2 \right)\cup \left[ 3;+\infty \right).

\left[ 3;4 \right].

\left[ 3;4 \right).

\left(-\infty ;-2 \right]\cup \left(3;+\infty \right).

Câu 10 (1đ):

Cho $A$ là tập hợp các số tự nhiên chẵn không lớn hơn $10$ , $B=\Big\{n \in \mathbb{N} \, \big| \, n \le 6 \Big\}$ , $C=\Big\{ n \in \mathbb{N} \, \big| \, 4 \le n \le 10 \Big\}$ . Tập hợp $A \cap \big(B \cup C \big)$ là

A\cap \big(B \cup C \big)=C

.

A\cap \big(B \cup C \big)=A

.

A\cap \big(B \cup C \big)=B

.

A\cap \big(B \cup C \big)=\varnothing

.

Câu 11 (1đ):

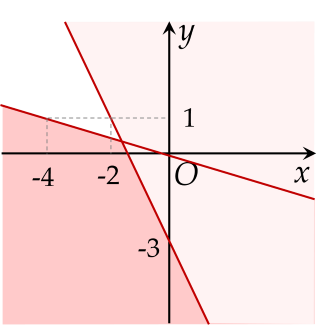
Phần không tô màu là hình vẽ biểu diễn miền nghiệm của hệ bất phương trình nào dưới đây?

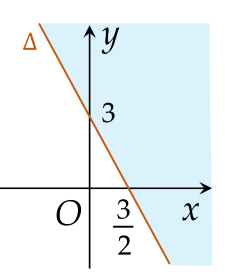
loading...

\left\{ \begin{aligned} & x+4y<0 \\ & 2x+y+3\le 0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x+4y\ge 0 \\ & 2x+y+3\ge 0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x+4y>0 \\ & 2x+y+3>0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x+4y>0 \\ & 2x+y+3\le 0 \\ \end{aligned} \right.

.

Câu 12 (1đ):

Phần tô màu (không bao gồm đường thẳng $\Delta$ ) trong hình vẽ là miền nghiệm của bất phương trình nào sau đây?

loading...

2x+y>3

.

2x+y<3

.

x+2y<3

.

x+2y>3

.

Câu 13 (1đ):

Cho $A$ là tập hợp các học sinh lớp 10 đang học ở trường X và $B$ là tập hợp các học sinh đang học môn Tiếng Anh của trường X.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $A\cap B$ là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường X.
b) $A\backslash B$ là tập hợp những học sinh lớp 10 và không học Tiếng Anh ở trường X.
c) $A\cup B$ là tập hợp các học sinh lớp 10 và học sinh học môn Tiếng Anh ở trường X.
d) $B \backslash A$ là tập hợp các học sinh học lớp 10 ở trường X nhưng không học môn Tiếng Anh.

Câu 14 (1đ):

Một đội sản xuất cần $3$ giờ để làm xong sản phẩm loại I và $2$ giờ để làm xong sản phẩm loại II. Biết thời gian tối đa cho việc sản xuất hai sản phẩm trên là $18$ giờ. Gọi $x, \, y$ lần lượt là số sản phẩm loại I, loại II mà đội làm được trong thời gian cho phép.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Tổng thời gian (giờ) làm xong sản phẩm loại $I$ là $2x$ , tổng thời gian làm xong sản phẩm loại II là $3y$ .
b) $3x+2y<18$ .
c) Khi số sản phẩm loại I là $3$ , loại II là $4$ thì thời gian đội đó làm nằm trong thời gian cho phép.
d) Khi số sản phẩm loại I là $2$ , loại II là $6$ thì thời gian đội đó làm vượt quá thời gian cho phép.

Câu 15 (1đ):

Cho $\overrightarrow{AB}=-\overrightarrow{CD}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng hướng.
b) $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng độ dài.
c) $ABCD$ là hình bình hành.
d) $\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{0}$ .

Câu 16 (1đ):

Cho $\sin \alpha =\dfrac{1}{3}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\cos^2 \alpha =\dfrac{8}{9}$ .
b) $A=\sin^2 \alpha + 3\cos^2 \alpha =\dfrac{35}{9}$ .
c) $B=5\sin^2 \alpha - \cos^2 \alpha =-\dfrac{1}{3}$ .
d) $C=\sqrt{\sin^2 \alpha + 3\cos^2 \alpha}+\sqrt{\cos^2 \alpha - 7\sin^2 \alpha}=2$ .

Câu 17 (1đ):

Cho hai tập khác rỗng $A=\left(m-1;4 \right]; \, B=\left(-2;2m+2 \right), \, m\in \mathbb{R}$ . Có bao nhiêu số nguyên $m$ để $A\cap B\ne \varnothing$ ?

Trả lời:

Câu 18 (1đ):

Trong đợt khảo sát nghề, giáo viên chủ nhiệm lớp 10D đưa ra ba nhóm ngành cho học sinh lựa chọn, đó là: Giáo dục, Y tế, Công nghệ thông tin. Học sinh có thể chọn từ một đến ba nhóm ngành nêu trên hoặc không chọn nhóm ngành nào trong ba nhóm ngành trên. Giáo viên chủ nhiệm thống kê theo từng nhóm ngành và được kết quả: có $6$ học sinh chọn nhóm ngành Giáo dục, $9$ học sinh chọn nhóm ngành Y tế, $10$ học sinh chọn nhóm ngành Công nghệ thông tin, $22$ học sinh không chọn nhóm ngành nào trong ba nhóm trên. Nếu thống kê số lượng học sinh chọn theo từng hai nhóm ngành được kết quả: có $3$ học sinh chọn hai nhóm ngành Giáo dục và Y tế, $2$ học sinh chọn hai nhóm ngành Y tế và Công nghệ thông tin, $3$ học sinh chọn hai nhóm ngành Giáo dục và Công nghệ thông tin. Có bao nhiêu học sinh chọn cả ba nhóm ngành nêu trên biết lớp 10D có $40$ học sinh?

Trả lời:

Câu 19 (1đ):

Cho tam giác $ABC$ có $A(0;3); \, B(-1;2); \, C(2;1)$ . Có bao nhiêu giá trị nguyên của tham số $m$ để điểm $M\Big(m;\dfrac{2m-1}{2}\Big)$ nằm bên trong tam giác $ABC$ ?

Trả lời:

Câu 20 (1đ):

Trong một cuộc thi pha chế đồ uống gồm hai loại là $A$ và $B$ , mỗi đội chơi được sử dụng tối đa $24$ g hương liệu, $9$ cốc nước lọc và $210$ g đường. Để pha chế một cốc đồ uống loại $A$ cần $1$ cốc nước lọc, $30$ g đường và $1$ g hương liệu. Để pha chế một cốc đồ uống loại $B$ cần $1$ cốc nước lọc, $10$ g đường và $4$ g hương liệu. Mỗi cốc đồ uống loại $A$ nhận được $6$ điểm thưởng, mỗi cốc đồ uống loại $B$ nhận được $8$ điểm thưởng. Để đạt được số điểm thưởng cao nhất, đội chơi cần pha chế $x$ cốc đồ uống loại $A$ , $y$ cốc đồ uống loại $B$ . Tính $x + y$ .

Trả lời:

Câu 21 (1đ):

Gọi $a$ , $b$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $L=y-x$ , với $x$ và $y$ thỏa mãn hệ bất phương trình $\left\{ \begin{aligned} & 2x+3y-6 \le 0 \\ & 2x-3y-1 \le 0 \\ & x \ge 0 \\ \end{aligned} \right.$ . Tính $11a+12b$ .

Trả lời:

Câu 22 (1đ):

Hai tàu đánh cá cùng xuất phát từ bến $A$ và đi thẳng đều về hai vùng biển khác nhau, theo hai hướng tạo với nhau góc $120^\circ$ . Tàu thứ nhất đi với tốc độ $8$ hải lí một giờ và tàu thứ hai đi với tốc độ $10$ hải lí một giờ.

loading...

Sau mấy giờ thì khoảng cách giữa hai tàu là $60$ hải lí? (Làm tròn kết quả đến chữ số thập phân thứ nhất)

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP