một phân xưởn sản xuất vải gồm 3 tổ .Tổ 2 và tổ 3 sản xuất được 35,6 m vải , tổ 2 hơn tổ 1 5,2 m . hỏi tổ 3 sản xuất được bao nhiêu mét vải , biết cả phân xưởng sản xuất được 47,8 m vải
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


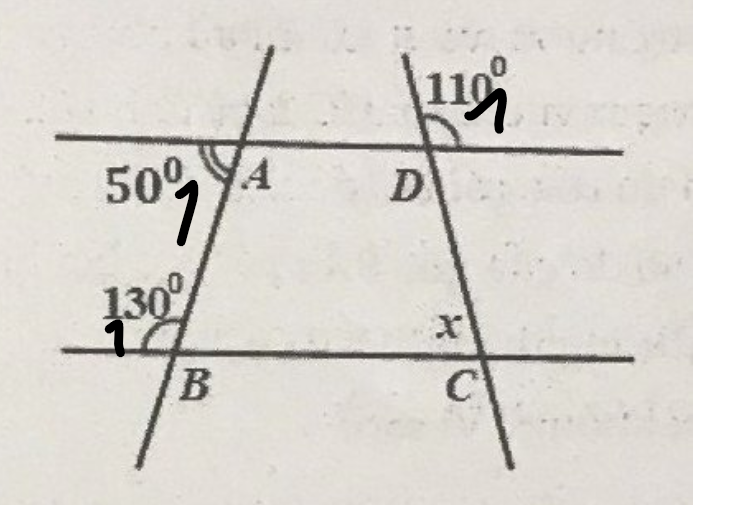
\(\widehat{A_1}+\widehat{BAD}=180^0\)
=>\(\widehat{BAD}+50^0=180^0\)
=>\(\widehat{BAD}=130^0\)
Ta có: \(\widehat{ADC}=\widehat{D_1}\)(hai góc đối đỉnh)
=>\(\widehat{ADC}=110^0\)
Ta có: \(\widehat{BAD}=\widehat{B_1}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
=>\(\widehat{ADC}+\widehat{DCB}=180^0\)
=>\(x+110^0=180^0\)
=>\(x=70^0\)
b)
\(\widehat{B}+\widehat{A}=130^o+50^o=180^o\)
Mà 2 góc này ở vị trí trong cùng phía
\(\Rightarrow BC//AD\Rightarrow\widehat{D}+\widehat{C}=180^o\)
\(\widehat{D}=110^o\) (đối đỉnh)
\(\Rightarrow\widehat{C}=180^o-110^o=70^o\)

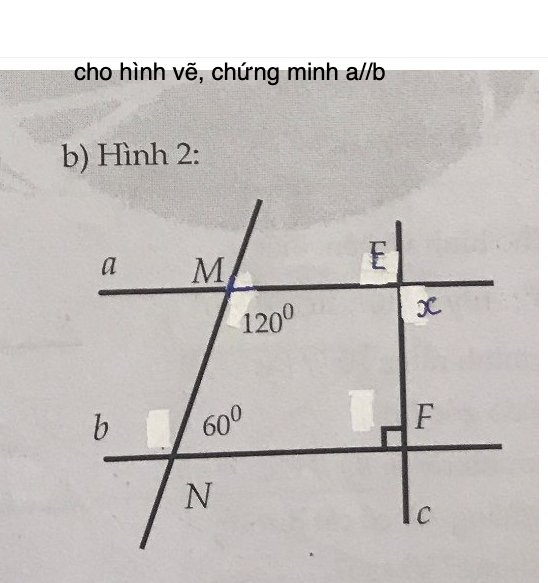
Ta có: \(\widehat{xMN}+\widehat{MNF}=120^0+60^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên a//b

ĐKXĐ: \(a\ne1\)
Để A là số nguyên thì \(a^3+2⋮a-1\)
=>\(a^3-1+3⋮a-1\)
=>\(3⋮a-1\)
=>\(a-1\in\left\{1;-1;3;-3\right\}\)
=>\(a\in\left\{2;0;4;-2\right\}\)

Ta có:
\(\widehat{M}=30^o< \widehat{N}=50^o< \widehat{P}=100^o\) (gt)
\(\Rightarrow NP< MP< MN\) (định lý)
Vậy...
Phần định lý kia nếu muốn đầy đủ thì bạn ghi là "quan hệ giữa góc và cạnh đối diện" nhé

a) xét tam giác ABC và tam giác ABD, có:
AC = AD (gt)
góc BAD = góc BAC (= 90 độ)
AB là cạnh chung
=> tam giác ABC = tam giác ABD (c-g-c)
b) xét tam giác MBC và tam giác MBD, có:
AB = AM (gt)
góc BAD = góc BAC (= 90 độ)
AC = AD (gt)
=> tam giác MBC = tam giác MBD (c-g-c)

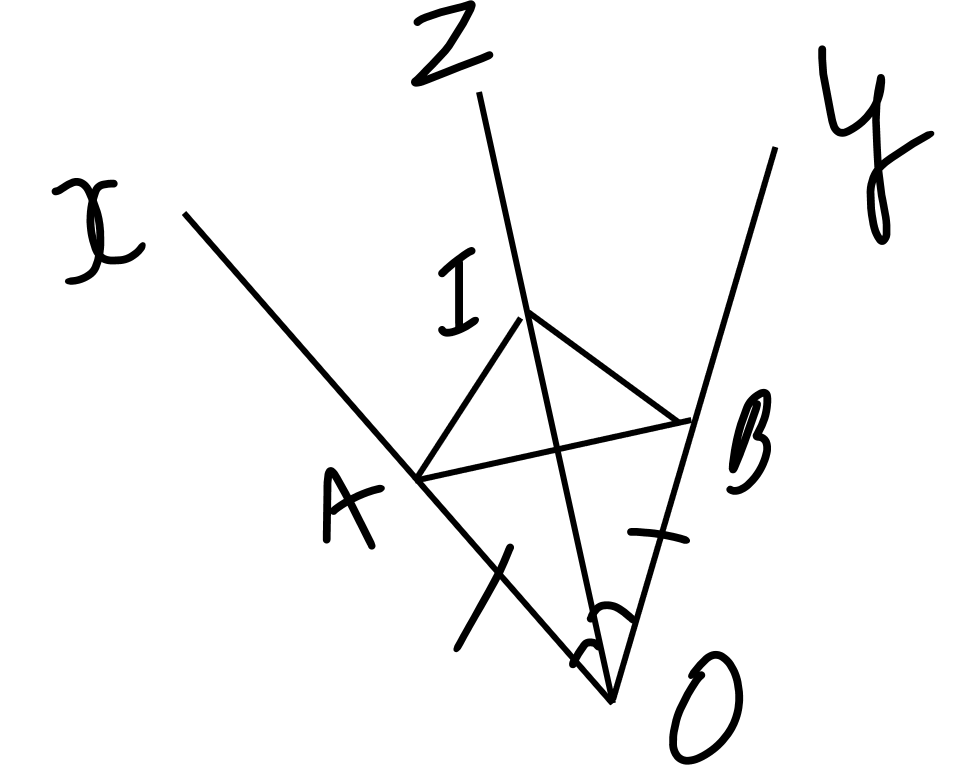
a) xét tam giác AOI và tam giác BOI, có:
OA = OB (gt)
góc AOI = góc BOI (vì I ∈ Oz, mà Oz là tia phân giác của xOy)
OI là cạnh chung
=> tam giác AOI = tam giác BOI (c-g-c)
b) ta có: OA = OB (gt)
=> tam giác AOB cân tại O
lại có OI là đường phân giác
=> OI cũng là đường cao
=> AB vuông góc với OI

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>DA=DE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAF=ΔDEC
=>DF=DC
=>ΔDFC cân tại D
c: ΔDAF=ΔDEC
=>AF=EC
ΔBAD=ΔBED
=>BA=BE
Ta có: BA+AF=BF
BE+EC=BC
mà BA=BE và AF=EC
nên BF=BC
=>ΔBFC cân tại B
Ta có: ΔBFC cân tại B
mà BH là đường phân giác
nên H là trung điểm của CF
CI=2DI
=>\(CI=\dfrac{2}{3}CD\)
Xét ΔCKF có
CD là đường trung tuyến
\(CI=\dfrac{2}{3}CD\)
Do đó: I là trọng tâm của ΔCKF
Xét ΔCKF có
I là trọng tâm
H là trung điểm của CF
Do đó: K,I,H thẳng hàng

Mình nghĩ đề là tìm x thuộc Z bạn nhé.
\(P=\dfrac{x+1}{2x-2}=\dfrac{x+1}{2\left(x-1\right)}\\ \Rightarrow2P=\dfrac{x+1}{x-1}=\dfrac{x-1+2}{x-1}=1+\dfrac{2}{x-1}\) (ĐK:x khác 1)
Để P đạt giá trị lớn nhất hiển nhiên 2P cũng phải đạt giá trị lớn nhất
\(\Rightarrow\dfrac{2}{x-1}\) đạt giá trị lớn nhất
\(\Rightarrow\) x-1 đạt GTNN và x-1>0
\(\Rightarrow\) x đạt GTNN và x>1
Lại có x nguyên do đó nên x=2 (TM)
Vậy x=2 thì P đạt GTLN
Đề bài thiếu điều kiện x nguyên nhé!
Ta có:
\(p=\dfrac{x+1}{2x-2}=\dfrac{x-1}{2\left(x-1\right)}+\dfrac{2}{2\left(x-1\right)}=\dfrac{1}{2}+\dfrac{1}{x-1}\) \(\left(x\ne1\right)\)
Để \(p\) đạt giá trị lớn nhất thì \(\dfrac{1}{x-1}\) đạt giá trị lớn nhất hay \(x-1\) đạt giá trị dương nhỏ nhất
Suy ra:
\(x-1=1\)
\(\Rightarrow x=2\)
Khi đó: \(p=\dfrac{1}{2}+\dfrac{1}{1}=\dfrac{3}{2}\)
Vậy...
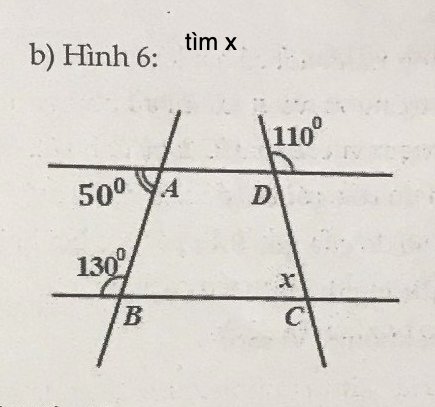
Số vải tổ 1 sản xuất được là:
\(47,8-35,6=12,2\left(m\right)\)
Số vải tổ 2 sản xuất được là:
\(12,2+5,2=17,4\left(m\right)\)
Số vải tổ 3 sản xuất được là:
\(35,6-17,4=18,2\left(m\right)\)