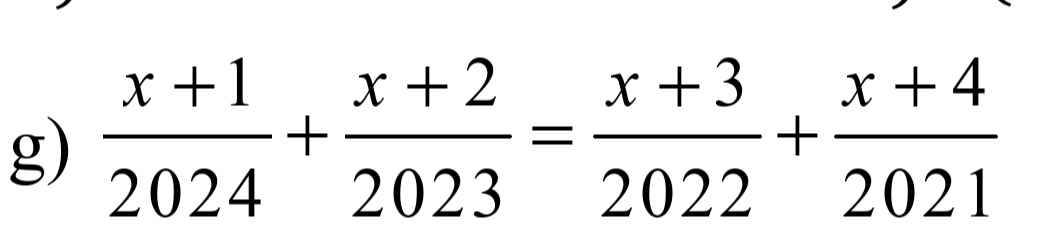 giải giúp mình với.mai mình phải thi rồi
giải giúp mình với.mai mình phải thi rồi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{ACB}\) chung
Do đó: ΔABC~ΔHAC
Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB~ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
b: Xét ΔEAB vuông tại A và ΔEFC vuông tại F có
\(\widehat{AEB}=\widehat{FEC}\)(hai góc đối đỉnh)
Do đó: ΔEAB~ΔEFC
=>\(\dfrac{EA}{EF}=\dfrac{EB}{EC}\)
=>\(EA\cdot EC=EB\cdot EF\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
=>\(\dfrac{AB}{BC}=\dfrac{HA}{AC}\)
=>\(AB\cdot AC=HA\cdot BC\)
b: Xét ΔAMH vuông tại M và ΔAHB vuông tại H có
\(\widehat{MAH}\) chung
Do đó: ΔAMH~ΔAHB
=>\(\dfrac{AM}{AH}=\dfrac{AH}{AB}\)
=>\(AH^2=AM\cdot AB\left(1\right)\)
Xét ΔANH vuông tại N và ΔAHC vuông tại H có
\(\widehat{NAH}\) chung
Do đó: ΔANH~ΔAHC
=>\(\dfrac{AN}{AH}=\dfrac{AH}{AC}\)
=>\(AN\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tạiA và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN~ΔACB
c:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot6\cdot8=24\left(cm^2\right)\)
Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>MN=AH
mà AH=4,8cm
nên MN=4,8(cm)
ΔAMN~ΔACB
=>\(\dfrac{S_{AMN}}{S_{ACB}}=\left(\dfrac{MN}{CB}\right)^2=\left(\dfrac{4.8}{10}\right)^2\)
=>\(S_{AMN}=\left(\dfrac{4.8}{10}\right)^2\cdot24=5,5296\left(cm^2\right)\)
\(S_{AMN}+S_{BMNC}=S_{ABC}\)
=>\(S_{BMNC}=24-5,5296=18,4704\left(cm^2\right)\)

`#3107.101107`
`a)`
`5 - (x - 6) = 4(2x - 3)`
\(\Leftrightarrow5-x+6=8x-12\)
\(\Leftrightarrow-x-8x=-12-5-6\)
\(\Leftrightarrow-9x=-23\)
\(\Leftrightarrow x=\dfrac{-23}{-9}=\dfrac{23}{9}\)
Vậy, \(x=\dfrac{23}{9}\)
`b)`
\(5\left(3x+2\right)-4\left(5-3x\right)=1\)
\(\Leftrightarrow15x+10-20+12x=1\)
\(\Leftrightarrow27x-10=1\)
\(\Leftrightarrow27x=11\)
\(\Leftrightarrow x=\dfrac{11}{27}\)
Vậy, \(x=\dfrac{11}{27}\)
`c)`
\(-4\left(x-3\right)=6x+\left(x-3\right)\)
\(\Leftrightarrow-4x+12=6x+x-3\)
\(\Leftrightarrow-4x-7x=-12-3\)
\(\Leftrightarrow11x=-15\)
\(\Leftrightarrow x=\dfrac{-15}{11}\)
Vậy, \(x=-\dfrac{15}{11}\)
`d)`
\(\dfrac{x}{3}-\dfrac{5x}{6}-\dfrac{5x}{12}=\dfrac{x}{4}-5\)
\(\Leftrightarrow\dfrac{4x}{12}-\dfrac{10x}{12}-\dfrac{5x}{12}=\dfrac{3x}{12}-\dfrac{60}{12}\)
\(\Leftrightarrow4x-10x-5x=3x-60\)
\(\Leftrightarrow-11x-3x=-60\)
\(\Leftrightarrow-14x=-60\)
\(\Leftrightarrow x=\dfrac{-60}{-14}=\dfrac{30}{7}\)
Vậy, \(x=\dfrac{30}{7}\)
`e)`
\(\dfrac{x-1}{2}-\dfrac{x+1}{15}-\dfrac{2x-13}{6}=0\)
\(\Leftrightarrow\dfrac{15\left(x-1\right)}{30}-\dfrac{2\left(x+1\right)}{30}-\dfrac{5\left(2x-13\right)}{30}=0\)
\(\Leftrightarrow15\left(x-1\right)-2\left(x+1\right)-5\left(2x-13\right)=0\)
\(\Leftrightarrow15x-15-2x-2-10x+65=0\)
\(\Leftrightarrow3x+48=0\)
\(\Leftrightarrow3x=-48\)
\(\Leftrightarrow x=-16\)
Vậy, \(x=-16.\)
`f)`
\(\dfrac{3\left(3-x\right)}{8}+\dfrac{2\left(5-x\right)}{3}=\dfrac{1-x}{2}-2\)
\(\Leftrightarrow\dfrac{9\left(3-x\right)}{24}+\dfrac{16\left(5-x\right)}{24}=\dfrac{12\left(1-x\right)}{24}-\dfrac{48}{24}\)
\(\Leftrightarrow27-9x+80-16x=12-12x-48\)
\(\Leftrightarrow-9x-16x+12x=12-48-27-80\)
\(\Leftrightarrow-13x=-143\)
\(\Leftrightarrow x=11\)
Vậy, `x = 11.`
`g)`
\(\dfrac{3\left(5x-2\right)}{4}-2=\dfrac{7x}{3}-5\left(x-7\right)\)
\(\Leftrightarrow\dfrac{9\left(5x-2\right)}{12}-\dfrac{24}{12}=\dfrac{28x}{12}-\dfrac{60\left(x-7\right)}{12}\)
\(\Leftrightarrow45x-18-24=28x-60x+420\)
\(\Leftrightarrow45x-28x+60x=42+420\)
\(\Leftrightarrow77x=462\)
\(\Leftrightarrow x=6\)
Vậy, `x = 6`
`h)`
\(\dfrac{x+5}{2}+\dfrac{3-2x}{4}=x-\dfrac{7+x}{6}\)
\(\Leftrightarrow\dfrac{6\left(x+5\right)}{12}+\dfrac{3\left(3-2x\right)}{12}=\dfrac{12x}{12}-\dfrac{2\left(7+x\right)}{12}\)
\(\Leftrightarrow6x+30+9-6x=12x-14-2x\)
\(\Leftrightarrow-10x=-53\)
\(\Leftrightarrow x=5,3\)
Vậy, `x = 5,3`
`i)`
\(\dfrac{x-3}{11}+\dfrac{x+1}{3}=\dfrac{x+7}{9}-1\)
\(\Leftrightarrow\dfrac{9\left(x-3\right)}{99}+\dfrac{33\left(x+1\right)}{99}=\dfrac{11\left(x+7\right)}{99}-\dfrac{99}{99}\)
\(\Leftrightarrow9x-27+33x+33=11x+77-99\)
\(\Leftrightarrow42x-11x=-22-6\)
\(\Leftrightarrow31x=-28\)
\(\Leftrightarrow x=-\dfrac{28}{31}\)
Vậy, \(x=-\dfrac{28}{31}.\)

a: 5+2x=20-3x
=>2x+3x=20-5
=>3x=15
=>\(x=\dfrac{15}{3}=5\)
b: \(7-\left(2x+4\right)=-\left(x+4\right)\)
=>\(7-2x-4+x+4=0\)
=>7-x=0
=>x=7
c: \(\left(5x+2\right)-3\left(2x+1\right)=-3x+7\)
=>\(5x+2-6x-3=-3x+7\)
=>-3x+7=-x-1
=>-2x=-8
=>x=4
d: \(2x-\left(3-5x\right)=4\left(x+3\right)\)
=>2x-3+5x=4x+12
=>7x-3=4x+12
=>3x=15
=>\(x=\dfrac{15}{3}=5\)
e: \(5\left(2x-3\right)-4\left(5x-7\right)=19-2\left(x+11\right)\)
=>\(10x-15-20x+28=19-2x-22\)
=>\(-10x+13=-2x-3\)
=>-8x=-16
=>x=2
f: \(x^2-\left(x+2\right)\left(x-2\right)=2x\)
=>\(x^2-\left(x^2-4\right)=2x\)
=>\(2x=x^2-x^2+4=4\)
=>\(x=\dfrac{4}{2}=2\)
g: \(\dfrac{1-3x}{6}+x-1=\dfrac{x+2}{2}\)
=>\(\dfrac{1-3x+6\left(x-1\right)}{6}=\dfrac{3x+6}{6}\)
=>1-3x+6x-6=3x+6
=>3x-5=3x+6
=>-5=6(loại)
h: \(\dfrac{3\left(2x+1\right)}{4}-5-\dfrac{3x+2}{10}=\dfrac{2\left(3x-1\right)}{5}\)
=>\(\dfrac{15\left(2x+1\right)-100-2\left(3x+2\right)}{20}=\dfrac{8\left(3x-1\right)}{20}\)
=>30x+15-100-6x-4=24x-8
=>24x-89=24x-8
=>-89=-8(vô lý)

a: 2x+6=0
=>2x=-6
=>x=-3
b: 4x+20=0
=>4x=-20
=>x=-5
c: 2(x+1)=5x-7
=>5x-7=2x+2
=>3x=9
=>x=3
d: \(2x-3=0\)
=>2x=3
=>\(x=\dfrac{3}{2}\)
e: 3x-1=x+3
=>3x-x=3+1
=>2x=4
=>\(x=\dfrac{4}{2}=2\)
f: 15-7x=9-3x
=>-7x+3x=9-15
=>-4x=-6
=>x=1,5
g: x-3=18
=>x=18+3=21
h: 2x+1=15-5x
=>2x+5x=15-1
=>7x=14
=>\(x=\dfrac{14}{7}=2\)
i: 3x-2=2x+5
=>3x-2x=2+5
=>x=7
k: -4x+8=0
=>-4x=-8
=>\(x=\dfrac{-8}{-4}=2\)
l: 2x+3=0
=>2x=-3
=>\(x=-\dfrac{3}{2}\)
m: 4x+5=3x
=>4x-3x=-5
=>x=-5

a: |x-4|=1
=>\(\left[{}\begin{matrix}x-4=1\\x-4=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\left(nhận\right)\\x=3\left(loại\right)\end{matrix}\right.\)
Khi x=5 thì \(B=\dfrac{5+1}{5-3}=\dfrac{6}{2}=3\)
b: \(A=\dfrac{x}{x-3}-\dfrac{x+1}{x+3}+\dfrac{3x-3}{9-x^2}\)
\(=\dfrac{x}{x-3}-\dfrac{x+1}{x+3}-\dfrac{3x-3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x\left(x+3\right)-\left(x+1\right)\left(x-3\right)-3x+3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2+3x-\left(x^2-2x-3\right)-3x+3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2+3-x^2+2x+3}{\left(x-3\right)\left(x+3\right)}=\dfrac{2x+6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x-3}\)
c: \(M=B:A=\dfrac{2}{x-3}:\dfrac{x}{x-3}=\dfrac{2}{x}\)
Để M=5 thì 2/x=5
=>\(x=\dfrac{2}{5}\left(nhận\right)\)
d: \(N=B-A=\dfrac{2}{x-3}-\dfrac{x}{x-3}=\dfrac{2-x}{x-3}\)
Để N là số nguyên thì \(2-x⋮x-3\)
=>\(x-2⋮x-3\)
=>\(x-3+1⋮x-3\)
=>\(1⋮x-3\)
=>\(x-3\in\left\{1;-1\right\}\)
=>\(x\in\left\{4;2\right\}\)

Bài 19:
Gọi số sản phẩm tổ 1 làm được trong tháng đầu là x(sản phẩm)
(Điều kiện: \(x\in Z^+\))
Số sản phẩm tổ 2 làm được trong tháng đầu là:
800-x(sản phẩm)
Số sản phẩm tổ 1 làm đươc trong tháng hai là:
\(\left(1+15\%\right)\cdot x=1,15x\left(sảnphẩm\right)\)
Số sản phẩm tổ 2 làm được trong tháng hai là:
\(\left(1+20\%\right)\left(800-x\right)=1,2\left(800-x\right)\left(sảnphẩm\right)\)
Tổng số sản phẩm hai tổ làm được trong tháng hai là 945 sản phẩm nên ta có:
1,15x+1,2(800-x)=945
=>1,15x+960-1,2x=945
=>-0,05x=-15
=>x=300(nhận)
Vậy: Trong tháng đầu, tổ 1 làm được 300 sản phẩm, tổ 2 làm được 800-300=500 sản phẩm

a: PA là đường cao ứng với đỉnh P của ΔMNP
=>PA\(\perp\)MN
b: Xét ΔMIN vuông tại I và ΔMAP vuông tại A có
\(\widehat{IMN}\) chung
Do đó: ΔMIN~ΔMAP
c: Xét ΔPIN vuông tại I và ΔPKM vuông tại K có
\(\widehat{IPN}\) chung
Do đó: ΔPIN~ΔPKM
=>\(\dfrac{PI}{PK}=\dfrac{PN}{PM}\)
=>\(\dfrac{PI}{PN}=\dfrac{PK}{PM}\)
Xét ΔPIK và ΔPNM có
\(\dfrac{PI}{PN}=\dfrac{PK}{PM}\)
\(\widehat{IPK}\) chung
Do đó: ΔPIK~ΔPNM
=>\(\widehat{PIK}=\widehat{PNM}\)
d: Xét ΔMIH vuông tại I và ΔMKP vuông tại K có
\(\widehat{IMH}\) chung
Do đó: ΔMIH~ΔMKP
=>\(\dfrac{MI}{MK}=\dfrac{MH}{MP}\)
=>\(MI\cdot MP=MH\cdot MK\)
e: \(\dfrac{PI}{PN}=\dfrac{PK}{PM}\)
=>\(PI\cdot PM=PK\cdot PN\)
\(MH\cdot MK+PK\cdot PN=PI\cdot PM+MI\cdot MP\)
\(=MP\left(PI+MI\right)=MP^2\)

Thay x=-1 và y=2 vào y=(3-2m)x+1, ta được:
-(3-2m)+1=2
=>-3+2m=1
=>2m=4
=>m=2


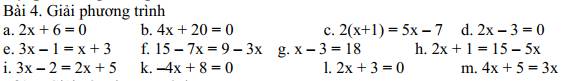
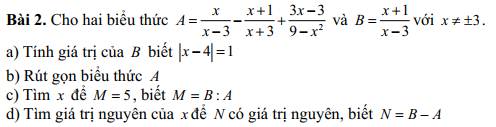


\(\dfrac{x+1}{2024}+\dfrac{x+2}{2023}=\dfrac{x+3}{2022}+\dfrac{x+4}{2021}\)
=>\(\left(\dfrac{x+1}{2024}+1\right)+\left(\dfrac{x+2}{2023}+1\right)=\left(\dfrac{x+3}{2022}+1\right)+\left(\dfrac{x+4}{2021}+1\right)\)
=>\(\dfrac{x+2025}{2024}+\dfrac{x+2025}{2023}=\dfrac{x+2025}{2022}+\dfrac{x+2025}{2021}\)
=>\(\left(x+2025\right)\left(\dfrac{1}{2024}+\dfrac{1}{2023}-\dfrac{1}{2022}-\dfrac{1}{2021}\right)=0\)
=>x+2025=0
=>x=-2025