Giải pt 6n4-4x2-2=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác BCEF có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BCEF là tứ giác nội tiếp

Lời giải:
a.
PT hoành độ giao điểm của $(P)$ và $(d)$ là:
$x^2=3x+m^2-1$
$\Leftrightarrow x^2-3x-(m^2-1)=0(*)$
Ta thấy:
$\Delta=9+4(m^2-1)=4m^2+5>0$ với mọi $m$
$\Rightarrow$ PT $(*)$ luôn có 2 nghiệm pb với mọi $m\in\mathbb{R}$
$\Rightarrow (P), (d)$ luôn cắt nhau tại 2 điểm pb với mọi $m\in\mathbb{R}$
b.
$x_1,x_2$ là hoành độ giao điểm của $(P), (d)$, tức là $x_1,x_2$ là nghiệm của $(*)$
Áp dụng định lý Viet:
$x_1+x_2=3$
$x_1x_2=1-m^2$
Khi đó:
$(x_1+1)(x_2+1)=1$
$\Leftrightarrow x_1x_2+(x_1+x_2)+1=1$
$\Leftrightarrow 1-m^2+3+1=1$
$\Leftrightarrow m^2=4\Leftrightarrow m=\pm 2$ (tm)

a: ΔOAB cân tại O
mà OH là đường trung tuyến
nên OH\(\perp\)AB tại H
Ta có: \(\widehat{OHS}=\widehat{OES}=\widehat{OFS}=90^0\)
=>O,H,S,E,F cùng thuộc đường tròn đường kính OS
b: Xét (O) có
\(\widehat{SEA}\) là góc tạo bởi tiếp tuyến ES và dây cung EA
\(\widehat{EBA}\) là góc nội tiếp chắn cung EA
Do đó: \(\widehat{SEA}=\widehat{EBA}\)
Xét ΔSEA và ΔSBE có
\(\widehat{SEA}=\widehat{SBE}\)
\(\widehat{ESA}\) chung
Do đó: ΔSEA~ΔSBE
=>\(\dfrac{SE}{SB}=\dfrac{SA}{SE}\)
=>\(SE^2=SA\cdot SB\)
a/ Ta có: ∠SEF = ∠SOF = 90° (do SE, SF là tiếp tuyến của đường tròn (O; R))
Do đó: ∠EHF = ∠SEF + ∠SOF = 180°
Suy ra: E, H, F cùng nằm trên một đường tròn. Vì ∠EHF = 180° nên H là tâm đường tròn đi qua E, F.
Ta có: ∠SHO = ∠SEO + ∠EOF = 90° + 90° = 180°
Suy ra: S, H, O cùng nằm trên một đường tròn. Vì ∠SHO = 180° nên H là tâm đường tròn đi qua S, O.
Vậy: S, E, H, O, F cùng nằm trên một đường tròn.
b/ Ta có: ∠ESB = ∠EAB (do ES, EB là tiếp tuyến của đường tròn (O; R))
Do đó: ∆ESB ~ ∆EAB (theo góc - cạnh - góc)
Suy ra: ES/EA = SB/AB
Vì H là trung điểm của AB nên AH = HB = AB/2
Suy ra: ES² = EA.AB = 2EA.AH = SA.SB (do EA = SA - AH)
c/ Ta có: SO = 3R = 6cm
Do đó: d = 2SO = 12cm
Suy ra: Diện tích hình tròn ngoại tiếp từ giác SEOF là: π(d/2)² = π(12/2)² = 36π (cm²)
d/ Ta có: ∠SEF = 90°
Do đó: mỗi cung EF = 90°/360° = 1/4
Suy ra: Diện tích hình quạt tròn giới hạn 2 bán kính SE, SF và cung nhỏ EF là: 1/4π(SE)² = 1/4πR² = 1/4π(2)² = π (cm²


c: OS=3*2=6(cm)
=>R1=6/2=3(cm)
Diện tích hình tròn ngoại tiếp tứ giác SEOF là \(3^2\cdot3,14=28,26\left(cm^2\right)\)

2: \(P=\left(\dfrac{\sqrt{x}+1}{x-\sqrt{x}}+\dfrac{\sqrt{x}-2}{x-1}\right):\dfrac{1}{x-1}\)
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{x-1}{1}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2+\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{x-1}{1}\)
\(=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}}{\sqrt{x}}=\dfrac{2x+1}{\sqrt{x}}\)
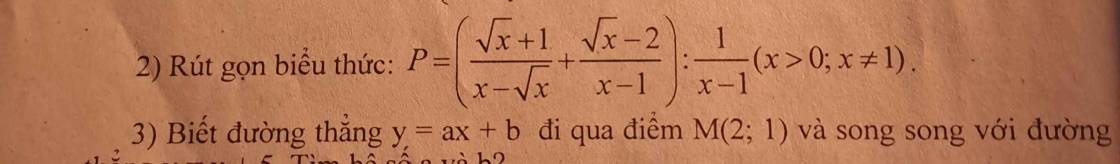
Sửa đề:
6x⁴ - 4x² - 2 = 0
⇔ 3x⁴ - 2x² - 1 = 0 (1)
Đặt t = x² (t ≥ 0)
(1) ⇔ 3t² - 2t - 1 = 0
Ta có:
a + b + c = 3 + (-2) + (-1) = 0
Phương trình có hai nghiệm:
t₁ = 1 (nhận); t₂ = -1/3 (loại)
Với t₁ = 1
⇒ x² = 1
⇔ x = -1 hoặc x = 1
Vậy S = {-1; 1}
6n4 - 4 \(\times\) 2 - 2 = 0
6n4 - 8 - 2 = 0
6n4 - 10 = 0
6n4 = 10
n4 = 10 : 6
n4 = \(\dfrac{5}{3}\)
n = \(\pm\) \(\sqrt[4]{\dfrac{5}{3}}\)
Vậy n = \(\pm\) \(\sqrt[4]{\dfrac{5}{3}}\)