 giúp em bài 5 vs ạ
giúp em bài 5 vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}+2⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3+5⋮\sqrt{x}-3\)
=>\(5⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;5;-5\right\}\)
=>\(\sqrt{x}\in\left\{4;2;8\right\}\)
=>\(x\in\left\{16;4;64\right\}\)

Thể tích phần bể chứa nước ban đầu là:
\(80\cdot50\cdot35=140000\left(cm^3\right)\)
Thể tích phần bể chứa nước lúc này sau khi thêm hòn đá là:
\(140000+20000=160000\left(cm^3\right)\)
Mực nước trong bể lúc này cao là:
\(160000:80:50=40\left(cm\right)\)
Thể tích ban đầu: 80 x 50 x 35 = 140.000 cm3
Sau khi thêm hòn đá: 140.000+20.000 = 160.000 cm3
=> Chiều cao mực nước = 160.000 / (80x50) = 40 cm

Độ dài cạnh huyền là:
\(\sqrt{3^2+7^2}=\sqrt{9+49}=\sqrt{58}\left(cm\right)\)
Bình phương cạnh huyền là:
32 + 72 = 58(cm2)
Cạnh huyền là: \(\sqrt{58}\) m

1: \(\left(x^2+2xy-3\right)\left(-xy^2\right)\)
\(=-xy^2\cdot x^2-xy^2\cdot2xy+3\cdot xy^2\)
\(=-x^3y^2-2x^2y^3+3xy^2\)
2: \(3x\left(x+2\right)-3x^2-12=0\)
=>\(3x^2+6x-3x^2-12=0\)
=>6x-12=0
=>6x=12
=>x=2
3: \(\left(2x^3-\dfrac{9}{2}x^2+\dfrac{1}{xy}\right)\cdot x^2y^3\)
\(=2x^3\cdot x^2y^3-\dfrac{9}{2}x^2\cdot x^2y^3+\dfrac{x^2y^3}{xy}\)
\(=2x^5y^3-\dfrac{9}{2}x^4y^3+xy^2\)
2; 3\(x\)(\(x+2\)) - 3\(x^2\) - 12 = 0
3\(x^2\) + 6\(x\) - 3\(x^2\) - 12 = 0
(3\(x^2\) - 3\(x^2\)) + 6\(x\) - 12 = 0
0 + 6\(x\) - 12 = 0
6\(x\) = 12
\(x\) = 12 : 6
\(x=2\)
Vậy \(x=2\)

a: \(-\dfrac{15}{19}=-1+\dfrac{4}{19}\)
\(-\dfrac{37}{41}=-1+\dfrac{4}{41}\)
\(-\dfrac{5}{9}=-1+\dfrac{4}{9}\)
\(\dfrac{23}{-27}=-\dfrac{23}{27}=-1+\dfrac{4}{27}\)
\(-\dfrac{7}{11}=-1+\dfrac{4}{11}\)
mà \(\dfrac{4}{41}< \dfrac{4}{27}< \dfrac{4}{19}< \dfrac{4}{11}< \dfrac{4}{9}\)
nên \(-\dfrac{37}{41}< -\dfrac{23}{27}< -\dfrac{15}{19}< -\dfrac{7}{11}< -\dfrac{5}{9}\)
mà \(-\dfrac{37}{41}< -\dfrac{76}{89}< -\dfrac{23}{27}\)
nên \(-\dfrac{37}{41}< -\dfrac{76}{89}< -\dfrac{23}{27}< -\dfrac{15}{19}< -\dfrac{7}{11}< -\dfrac{5}{9}\)

Sửa đề: \(\dfrac{1}{5}< \dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4}\)
Đặt \(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}\)
\(\dfrac{1}{5}-\dfrac{1}{6}< \dfrac{1}{5\cdot6}< \dfrac{1}{5^2}< \dfrac{1}{4\cdot5}=\dfrac{1}{4}-\dfrac{1}{5}\)
\(\dfrac{1}{6}-\dfrac{1}{7}< \dfrac{1}{6\cdot7}< \dfrac{1}{6^2}< \dfrac{1}{5\cdot6}=\dfrac{1}{5}-\dfrac{1}{6}\)
...
\(\dfrac{1}{100}-\dfrac{1}{101}=\dfrac{1}{100\cdot101}< \dfrac{1}{100^2}< \dfrac{1}{100\cdot99}=\dfrac{1}{99}-\dfrac{1}{100}\)
Do đó: \(\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{100}-\dfrac{1}{101}< \dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
=>\(\dfrac{1}{5}-\dfrac{1}{101}< A< \dfrac{1}{4}-\dfrac{1}{100}\)
=>\(\dfrac{1}{5}< A< \dfrac{1}{4}\)
A = \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + \(\dfrac{1}{7^2}\) + ... + \(\dfrac{1}{100^2}\)
\(\dfrac{1}{5.6}\) < \(\dfrac{1}{5^2}\) < \(\dfrac{1}{4.5}\)
\(\dfrac{1}{6.7}\) < \(\dfrac{1}{6^2}\) < \(\dfrac{1}{5.6}\)
\(\dfrac{1}{7.8}\) < \(\dfrac{1}{7^2}\) < \(\dfrac{1}{6.7}\)
......................
\(\dfrac{1}{100.101}\) < \(\dfrac{1}{100^2}\) < \(\dfrac{1}{99.100}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5.6}\) + \(\dfrac{1}{6.7}\) + ... + \(\dfrac{1}{100.101}\)< \(\dfrac{1}{5^2}\)+\(\dfrac{1}{6^2}\)+...+\(\dfrac{1}{100^2}\)<\(\dfrac{1}{4.5}\)+\(\dfrac{1}{5.6}\)+...+\(\dfrac{1}{99.100}\)
\(\dfrac{1}{5}\)-\(\dfrac{1}{6}\)+\(\dfrac{1}{6}\)-\(\dfrac{1}{7}\)+\(\dfrac{1}{100}\)-\(\dfrac{1}{101}\) < \(\dfrac{1}{5^2}\)+\(\dfrac{1}{6^2}\)+...+\(\dfrac{1}{100^2}\)< \(\dfrac{1}{4}\)-\(\dfrac{1}{5}\)+\(\dfrac{1}{5}\)-\(\dfrac{1}{6}\)+...+\(\dfrac{1}{99}\)-\(\dfrac{1}{100}\)
\(\dfrac{1}{5}\) - \(\dfrac{1}{101}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\)+...+\(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) - \(\dfrac{1}{100}\)
\(\dfrac{6}{30}\) - \(\dfrac{1}{101}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\)+ .... + \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) - \(\dfrac{1}{100}\) < \(\dfrac{1}{4}\)
\(\dfrac{5}{30}\) +( \(\dfrac{1}{30}\) - \(\dfrac{1}{101}\)) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + ... + \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\)
\(\dfrac{1}{6}\) + (\(\dfrac{1}{30}\) - \(\dfrac{1}{101}\)) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + ... + \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\)
Vì \(\dfrac{1}{30}\) > \(\dfrac{1}{101}\) ⇒ \(\dfrac{1}{30}\) - \(\dfrac{1}{101}\) > 0 ⇒ \(\dfrac{1}{6}\) + (\(\dfrac{1}{30}\) - \(\dfrac{1}{101}\)) > \(\dfrac{1}{6}\)
Vậy \(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + ... + \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) (đpcm)
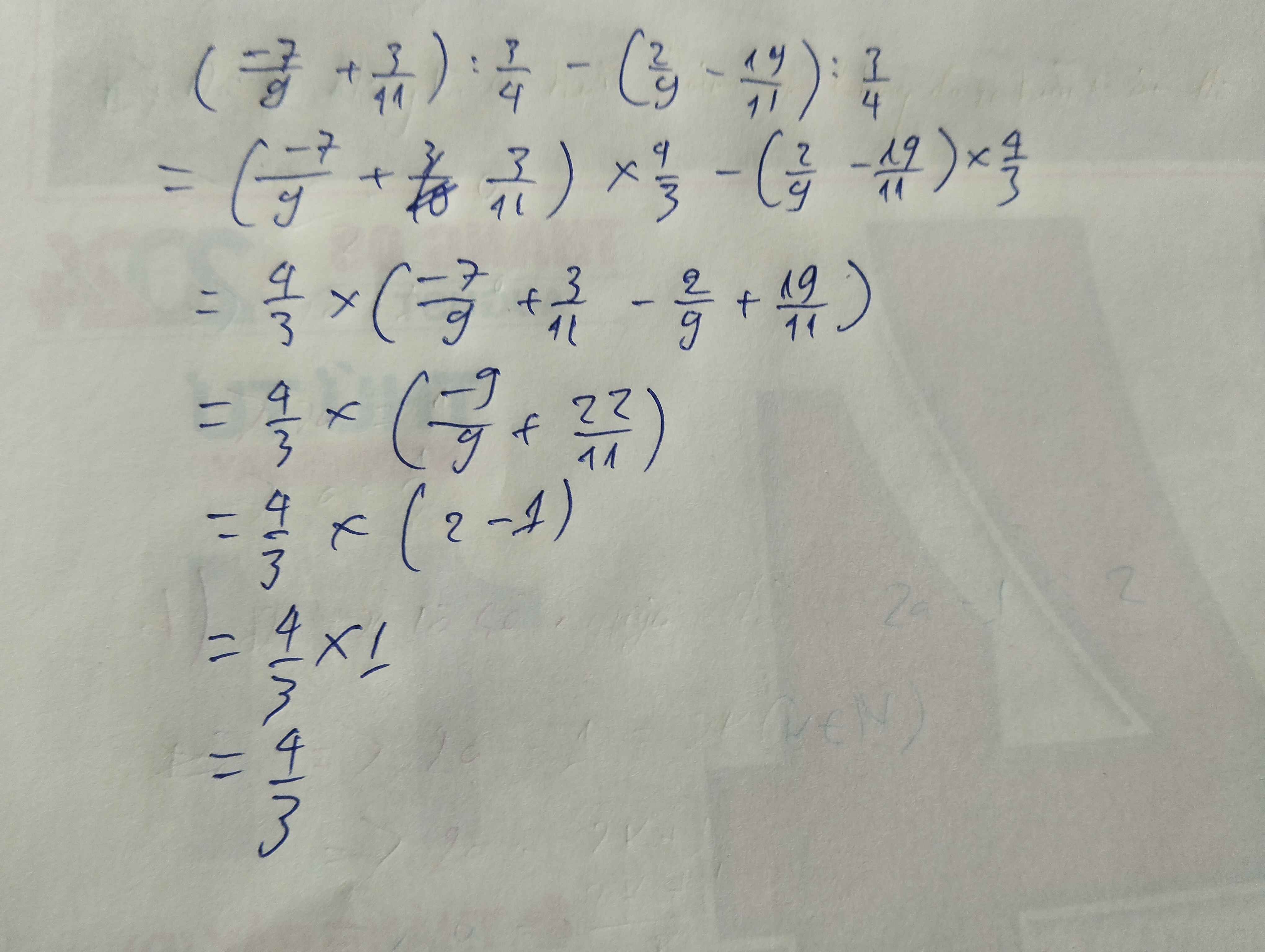
Bài 5:
a: \(\left|-\dfrac{3}{5}+\dfrac{1}{2}\right|-\left(\dfrac{3}{4}-\dfrac{5}{8}\right)+\left|-\dfrac{3}{2}\right|\)
\(=\left|-\dfrac{6}{10}+\dfrac{5}{10}\right|-\dfrac{1}{8}+\dfrac{3}{2}\)
\(=\dfrac{1}{10}-\dfrac{1}{8}+\dfrac{3}{2}=\dfrac{4}{40}-\dfrac{5}{40}+\dfrac{60}{40}=\dfrac{59}{40}\)
b: \(\dfrac{2}{3}-\left|-\dfrac{7}{3}+\dfrac{3}{4}\right|-\left|-\dfrac{5}{2}+1\right|\)
\(=\dfrac{2}{3}-\left|-\dfrac{28}{12}+\dfrac{9}{12}\right|-\left|-\dfrac{5}{2}+\dfrac{2}{2}\right|\)
\(=\dfrac{2}{3}-\dfrac{19}{12}-\dfrac{3}{2}=\dfrac{8}{12}-\dfrac{19}{12}-\dfrac{18}{12}\)
\(=-\dfrac{29}{12}\)
c: \(\dfrac{1}{5}-\left(\dfrac{3}{10}-\dfrac{-3}{5}\right)-\left|\dfrac{1}{4}-\dfrac{2}{5}\right|\)
\(=\dfrac{1}{5}-\dfrac{3}{10}-\dfrac{3}{5}-\left|\dfrac{5}{20}-\dfrac{8}{20}\right|\)
\(=-\dfrac{7}{10}-\left|\dfrac{-3}{20}\right|=-\dfrac{7}{10}-\dfrac{3}{20}=-\dfrac{17}{20}\)
d: \(\left|-\dfrac{5}{2}+\dfrac{3}{4}-\dfrac{1}{3}\right|-\left(-\dfrac{3}{4}+\dfrac{-5}{3}\right)\)
\(=\left|-\dfrac{30}{12}+\dfrac{9}{12}-\dfrac{4}{12}\right|+\dfrac{3}{4}+\dfrac{5}{3}\)
\(=\dfrac{25}{12}+\dfrac{9}{12}+\dfrac{20}{12}=\dfrac{54}{12}=\dfrac{9}{2}\)