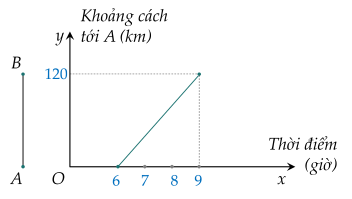
y/(2 - y) + (y ^ 2 + 2y)/(2y + 2) * ((y + 2)/(y ^ 2 - 2y) - y/(y ^ 2 - 4))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

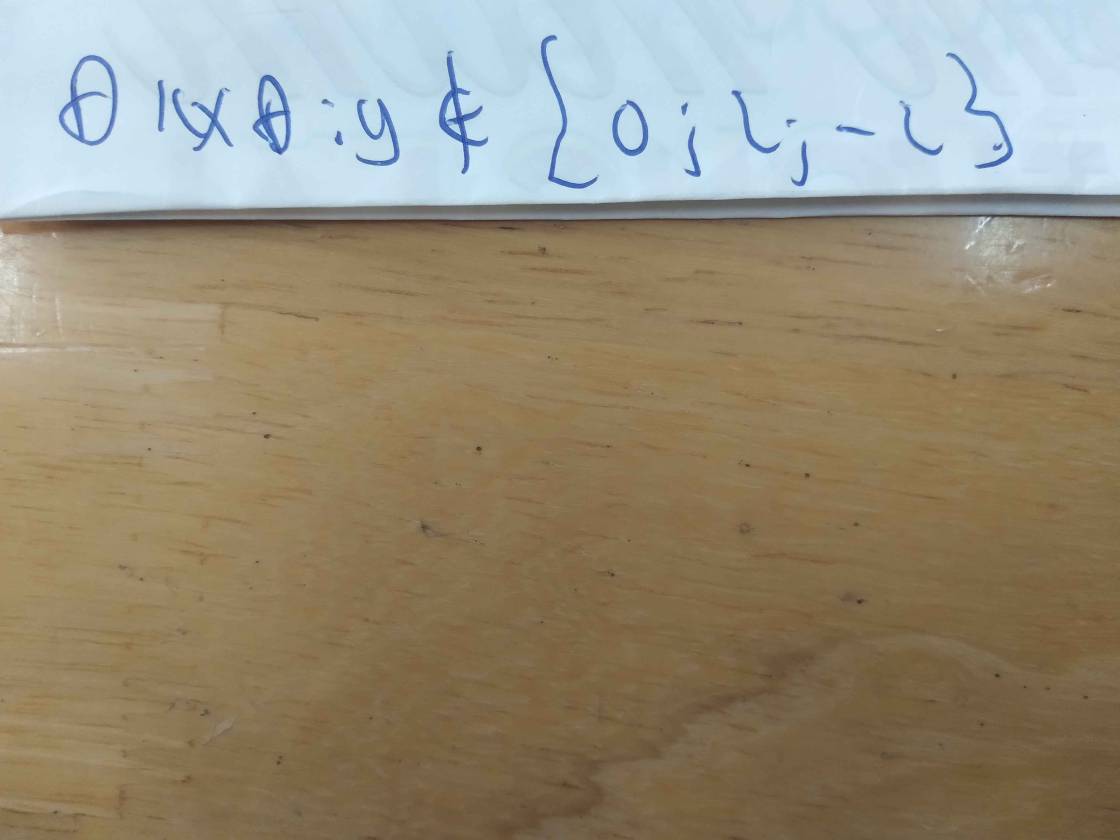




1: \(x^4+3x^2-4=0\)
=>\(x^4+4x^2-x^2-4=0\)
=>\(\left(x^2+4\right)\left(x^2-1\right)=0\)
=>\(x^2-1=0\)
=>\(x^2=1\)
=>\(x=\pm1\)
2: \(\left(x^2-2x\right)^2+\left|x^2-2x\right|-2=0\)
=>\(\left(\left|x^2-2x\right|\right)^2+\left|x^2-2x\right|-2=0\)
=>\(\left(\left|x^2-2x\right|+2\right)\left(\left|x^2-2x\right|-1\right)=0\)
=>\(\left|x^2-2x\right|-1=0\)
=>\(\left[{}\begin{matrix}x^2-2x=1\\x^2-2x=-1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x^2-2x-1=0\\x^2-2x+1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left(x-1\right)^2-2=0\\\left(x-1\right)^2=0\end{matrix}\right.\)
=>\(x\in\left\{1;\pm\sqrt{2}+1\right\}\)
3: ĐKXĐ: \(x\notin\left\{-2;-1\right\}\)
\(\dfrac{x}{x+2}< \dfrac{x}{x+1}\)
=>\(\dfrac{x}{x+2}-\dfrac{x}{x+1}< 0\)
=>\(\dfrac{x\left(x+1\right)-x\left(x+2\right)}{\left(x+2\right)\left(x+1\right)}< 0\)
=>\(\dfrac{-x}{\left(x+2\right)\left(x+1\right)}< 0\)
=>\(\dfrac{x}{\left(x+1\right)\left(x+2\right)}>0\)
TH1: \(\left\{{}\begin{matrix}x>0\\\left(x+1\right)\left(x+2\right)>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>0\\\left[{}\begin{matrix}x>-1\\x< -2\end{matrix}\right.\end{matrix}\right.\)
=>\(x>0\)
TH2: \(\left\{{}\begin{matrix}x< 0\\\left(x+1\right)\left(x+2\right)< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 0\\-2< x< -1\end{matrix}\right.\)
=>-2<x<-1
1.
$x^4+3x^2-4=0$
$\Leftrightarrow (x^4-x^2)+(4x^2-4)=0$
$\Leftrightarrow x^2(x^2-1)+4(x^2-1)=0$
$\Leftrightarrow (x^2-1)(x^2+4)=0$
$\Leftrightarrow x^2-1=0$ hoặc $x^2+4=0$
Nếu $x^2-1=0\Leftrightarrow x^2=1\Leftrightarrow x=\pm 1$
Nếu $x^2+4=0\Leftrightarrow x^2=-4<0$ (vô lý)
Vậy pt có nghiệm $x=1$ hoặc $x=-1$

mịa đang học đột nhiên lag sau đó văng mẹ rồi vào lại thì bắt đătf từ đầu

Gọi ba số tự nhiên liên tiếp lần lượt là x;x+1;x+2
Cộng ba tích, mỗi tích của tích của hai trong ba số trên thì được 26 nên ta có:
\(x\left(x+1\right)+\left(x+1\right)\left(x+2\right)+x\left(x+2\right)=26\)
=>\(x^2+x+x^2+3x+2+x^2+2x=26\)
=>\(3x^2+6x+2-26=0\)
=>\(3x^2+6x-24=0\)
=>\(x^2+2x-8=0\)
=>(x+4)(x-2)=0
=>\(\left[{}\begin{matrix}x=-4\left(loại\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
Vậy: Ba số liên tiếp cần tìm là 2;3;4
Giải:
Ba số tự nhiên liên tiếp có dạng: n; n + 1; n + 2 (n \(\in\) N*)
Tích của số thứ nhất và số thứ hai là: n.(n + 1)
Tích của số thứ nhất và số thứ ba là: n.(n + 2)
Tích của số thứ hai và số thứ ba là: (n + 1).(n + 2)
Theo bài ra ta có:
n(n + 1) + n(n+2) + (n + 1)(n + 2) = 26
n2 + n + n2 + 2n + n2 + n + 2n + 2 = 26
3n2 + 6n + 2 - 26 = 0
3n2 + 6n - 24 = 0
3n2 - 12 + 6n - 12= 0
(3n2 - 12) + (6n - 12) = 0
3(n2 - 4) + 6(n - 2) = 0
3(n - 2)(n + 2) + 6(n - 2) = 0
(n - 2)(3n + 6 + 6) = 0
(n - 2)(3n + 12) = 0
\(\left[{}\begin{matrix}n-2=0\\3n+12=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}n=2\\n=-4\end{matrix}\right.\)
n = - \(4\) (loại)
Vậy n = 2, nên số thứ nhất là 2
Kết luận: Ba số tự nhiên liên tiếp đó là: 2; 3; 4

a) \(\left(3x+5\right)^3+\left(2x-7\right)^3-\left(5x-2\right)^3=0\)
\(\Leftrightarrow\left[\left(3x+5\right)+\left(2x-7\right)\right]\left[\left(3x+5\right)^2-\left(3x+5\right)\left(2x-7\right)+\left(2x-7\right)^2\right]-\left(5x-2\right)^3=0\)
\(\Leftrightarrow\left(5x-2\right)\left[9x^2+30x+25-\left(6x^2-21x+10x-35\right)+4x^2-28x+49\right]-\left(5x-2\right)^3=0\)
\(\Leftrightarrow\left(5x-2\right)\left(7x^2+13x+109\right)-\left(5x-2\right)^3=0\)
\(\Leftrightarrow\left(5x-2\right)\left[7x^2+13x+109-\left(5x-2\right)^2\right]=0\)
\(\Leftrightarrow\left(5x-2\right)\left(7x^2+13x+109-25x^2+20x-4\right)=0\)
\(\Leftrightarrow\left(5x-2\right)\left(-18x^2+33x+105\right)=0\)
\(\Leftrightarrow-3\left(5x-2\right)\left(6x^2-11x-35\right)=0\)
\(\Leftrightarrow-3\left(5x-2\right)\left(6x^2+10x-21x-35\right)=0\)
\(\Leftrightarrow-3\left(5x-2\right)\left[2x\left(3x+5\right)-7\left(3x+5\right)\right]=0\)
\(\Leftrightarrow-3\left(5x-2\right)\left(2x-7\right)\left(3x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-2=0\\2x-7=0\\3x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{5}\\x=\dfrac{7}{2}\\x=-\dfrac{5}{3}\end{matrix}\right.\)
a: Đặt \(3x+5=a;2x-7=b\)
=>a+b=3x+5+2x-7=5x-2
Phương trình ban đầu sẽ trở thành:
\(a^3+b^3-\left(a+b\right)^3=0\)
=>\(\left(a+b\right)^3-3ab\left(a+b\right)-\left(a+b\right)^3=0\)
=>-3ab(a+b)=0
=>ab(a+b)=0
=>(3x+5)(2x-7)(5x-2)=0
=>\(\left[{}\begin{matrix}3x+5=0\\2x-7=0\\5x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{3}\\x=\dfrac{7}{2}\\x=\dfrac{2}{5}\end{matrix}\right.\)
b: \(\left(x^2+x-2\right)^3+\left(x^2+5x+6\right)^3-8\left(x^2+3x+2\right)^3=0\)
=>\(\left(x^2+x-2\right)^3+\left(x^2+5x+6\right)^3-\left(2x^2+6x+4\right)^3=0\)(2)
Đặt \(x^2+x-2=c;x^2+5x+6=d\)
=>\(c+d=2x^2+6x+4\)
Phương trình (2) sẽ trở thành:
\(c^3+d^3-\left(c+d\right)^3=0\)
=>\(\left(c+d\right)^3-3cd\left(c+d\right)-\left(c+d\right)^3=0\)
=>-3cd(c+d)=0
=>cd(c+d)=0
=>\(\left(x^2+x-2\right)\left(x^2+5x+6\right)\left(2x^2+6x+4\right)=0\)
=>\(\left(x+2\right)\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+2\right)\left(x+1\right)=0\)
=>\(\left(x+2\right)^3\cdot\left(x-1\right)\left(x+1\right)\left(x+3\right)=0\)
=>\(\left[{}\begin{matrix}x=-2\\x=1\\x=-1\\x=-3\end{matrix}\right.\)

a:
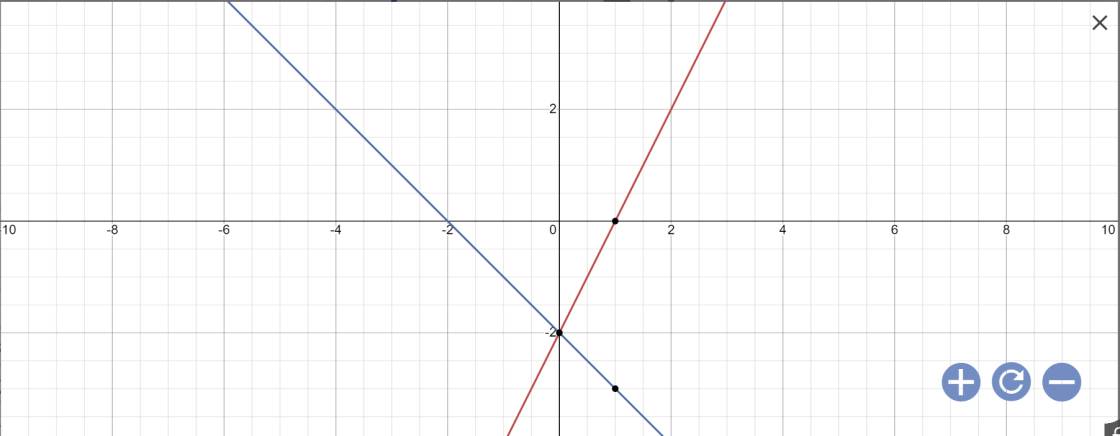
b: Tọa độ A là:
\(\left\{{}\begin{matrix}2x-2=-x-2\\y=2x-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=0\\y=2x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0-2=-2\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\2x-2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\2x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\-x-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x+2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
Vậy: A(0;-2); B(1;0); C(-2;0)
\(AB=\sqrt{\left(1-0\right)^2+\left(0+2\right)^2}=\sqrt{5}\)
\(AC=\sqrt{\left(-2-0\right)^2+\left(0+2\right)^2}=2\sqrt{2}\)
\(BC=\sqrt{\left(-2-1\right)^2+\left(0-0\right)^2}=3\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{5+8-9}{2\cdot\sqrt{5}\cdot2\sqrt{2}}=\dfrac{4}{4\sqrt{10}}=\dfrac{1}{\sqrt{10}}\)
=>\(sinBAC=\sqrt{1-\left(\dfrac{1}{\sqrt{10}}\right)^2}=\dfrac{3}{\sqrt{10}}\)
Diện tích tam giác BAC là:
\(S_{BAC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=\dfrac{1}{2}\cdot\sqrt{5}\cdot2\sqrt{2}\cdot\dfrac{3}{\sqrt{10}}\)
\(=3\)

1: Xét ΔPMN có AB//MN
nên \(\dfrac{AB}{MN}=\dfrac{PA}{PM}\)
=>\(\dfrac{AB}{MN}=\dfrac{3}{7}\)
mà MN-AB=8
nên \(MN=8:\left(7-3\right)\cdot7=8:4\cdot7=14\left(cm\right)\)
=>AB=14-8=6(cm)
2:
a: Xét ΔABD có AE là phân giác
nên \(\dfrac{BE}{ED}=\dfrac{BA}{AD}\)
Xét ΔBAC có BF là phân giác
nên \(\dfrac{FA}{FC}=\dfrac{BA}{BC}=\dfrac{BA}{AD}\)
=>\(\dfrac{BE}{ED}=\dfrac{FA}{FC}\)
b:
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
\(\dfrac{BE}{ED}=\dfrac{FA}{FC}\)
=>\(\dfrac{BE}{ED}+1=\dfrac{FA}{FC}+1\)
=>\(\dfrac{BD}{ED}=\dfrac{AC}{FC}\)
mà BD=2OD và AC=2OC
nên \(\dfrac{2OD}{ED}=\dfrac{2OC}{FC}\)
=>\(\dfrac{OD}{ED}=\dfrac{OC}{FC}\)
Xét ΔODC có \(\dfrac{OD}{ED}=\dfrac{OC}{FC}\)
nên EF//CD

a: Đặt (d): y=ax+b
Theo đồ thị, ta sẽ thấy: (d) đi qua A(6;0) và B(9;120)
Thay x=6 và y=0 vào y=ax+b, ta được:
\(a\cdot6+b=0\)
=>6a+b=0(1)
Thay x=9 và y=120 vào y=ax+b, ta được:
\(a\cdot9+b=120\)
=>9a+b=120(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}9a+b=120\\6a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9a+b-6a-b=120\\6a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a=120\\b=-6a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=40\\b=-240\end{matrix}\right.\)
b: a=40; b=-240
=>y=40x-240
Thay x=8 vào y=40x-240, ta được:
\(y=40\cdot8-240=80\left(km\right)\)
=>Ô tô còn cách B 120-80=40km