1: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔBAD=ΔBED

2: ta có; ΔBAD=ΔBED
=>DA=DE
mà DE<DC(ΔDEC vuông tại E)

nên DA<DC

a: Xét ΔDAF và ΔDBE có

DA=DB

\(\widehat{ADF}\) chung

DF=DE

Do đó: ΔDAF=ΔDBE

b: Ta có: DA+AE=DE

DB+BF=DF

mà DA=DB và DE=DF

nên AE=BF

Xét ΔAEF và ΔBFE có

AE=BF

\(\widehat{AEF}=\widehat{BFE}\)

FE chung

Do đó: ΔAEF=ΔBFE

=>\(\widehat{AFE}=\widehat{BEF}\)

=>\(\widehat{IEF}=\widehat{IFE}\)

=>IE=IF

Xét ΔDEI và ΔDFI có

DE=DF

EI=FI

DI chung

Do đó: ΔDEI=ΔDFI

=>\(\widehat{EDI}=\widehat{FDI}\)

=>DI là phân giác của góc EDF

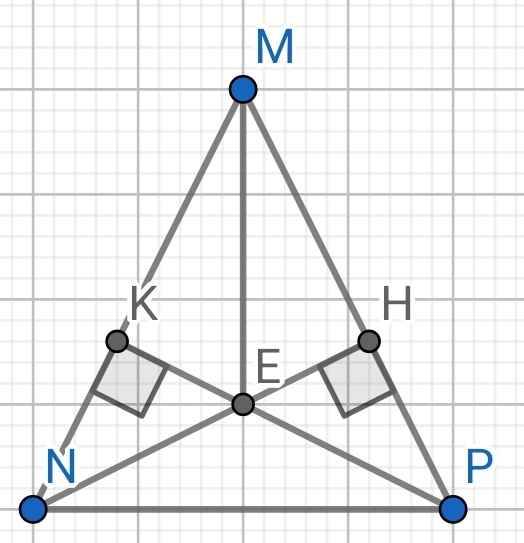
a) Do ∆MNP cân tại M (gt)

⇒ ∠MPN = ∠MNP

⇒ ∠HPN = ∠KNP

Xét hai tam giác vuông: ∆NHP và ∆PKN có:

NP là cạnh chung

∠HPN = ∠KNP (cmt)

⇒ ∆NHP = ∆PKN (cạnh huyền - góc nhọn)

b) Do ∆NHP = ∆PKN (cmt)

⇒ ∠HNP = ∠KPN (hai góc tương ứng)

⇒ ∠ENP = ∠EPN

∆ENP có:

∠ENO = ∠EPN (cmt)

⇒ ∆ENP cân tại E

c) ∆MNP có hai đường cao NH và PK cắt nhau tại E

⇒ ME là đường cao thứ ba của ∆MNP

Mà ∆MNP cân tại M (gt)

⇒ ME vừa là đường cao cũng vừa là đường phân giác của ∆MNP

⇒ ME là tia phân giác của ∠NMP

Câu 16:

a: Xét ΔBAH và ΔBDH có

BA=BD

AH=DH

BH chung

Do đó: ΔBAH=ΔBDH

b: ΔBAH=ΔBDH

=>\(\widehat{ABH}=\widehat{DBH}\)

Xét ΔBAE và ΔBDE có

BA=BD

\(\widehat{ABE}=\widehat{DBE}\)

BE chung

Do đó: ΔBAE=ΔBDE

=>EA=ED
=>ΔEAD cân tại E

c: ta có: ED=EA

mà EA<EM(ΔEAM vuông tại A)

nên ED<EM

Câu 13:

a: Đặt P(x)=0

=>x-5=0

=>x=5

Đặt M(x)=0

=>2x+4=0

=>2x=-4

=>x=-2

b: \(A\left(-3\right)=2\cdot\left(-3\right)+6=-6+6=0\)

=>x=-3 là nghiệm của A(x)

c: B(2)=-6

=>\(a\cdot2+4=-6\)

=>2a=-10

=>a=-5

TK:

Để chứng minh rằng \( BE \) vuông góc với \( AC \), ta sẽ sử dụng các định lí về tam giác vuông và tính chất của phân giác trong tam giác.

Vì tam giác \( ABC \) vuông tại \( A \), nên phân giác \( BE \) sẽ chia góc \( CAB \) thành hai góc nhỏ bằng nhau, tức là \( \angle BAE = \angle CAE \).

Vì \( EH \) là đường cao của tam giác \( BEC \), nên \( EH \) vuông góc với \( BC \).

Xét tam giác \( BEH \) và \( CEA \):
- \( \angle BEH = \angle CEA \) (vì cùng là góc phân giác)
- \( \angle EHB = \angle EAC \) (vì \( EH \) song song với \( AC \))
- \( EH \) vuông góc với \( BC \) và \( AC \) (do phân giác chia góc \( CAB \))
=> \( BE \) là đường cao của tam giác \( BEC \) (theo tính chất của tam giác vuông).
=> \( BE \) vuông góc với \( AC \), vì đường cao luôn vuông góc với đáy của tam giác.

Vậy, ta đã chứng minh được rằng \( BE \) vuông góc với \( AC \).

Sửa đề; Chứng minh BE\(\perp\)KC

Xét ΔBKC có

CA,KH là các đường cao

CA cắt KH tại E

Do đó: E là trực tâm của ΔBKC

=>BE\(\perp\)KC

A(x)+B(x)= x^3 + 2x^2 -x+1+2x^3 +3x^2 +4x +5

= ( x^3 +2x^3) + ( 2x^2 + 3x^2) + ( -x +4x ) + ( 1 +5) 

= 3x^3 + 5x^2 + 3x +6

A(x) - B(x) = x^3 +2x^2 -x+1 - 2x^3 - 3x^2 -4x-5

= (x^3 - 2x^3) + ( 2x^2 - 3x^2) + ( -x -4x ) + ( 1-5)

= -x^3 - x^2 - 5x-4

 Đây nha bạn :)

a: Xét ΔAIB và ΔAIC có

AI chung

IB=IC

AB=AC

Do đó: ΔAIB=ΔAIC

b: ΔABC cân tại A

=>\(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy)

Bài 1:

a: \(A\left(x\right)=2x^4+3x^2-x+3-x^2-x^4-6x^3\)

\(=\left(2x^4-x^4\right)-6x^3+\left(3x^2-x^2\right)-x+3\)

\(=x^4-6x^3+2x^2-x+3\)

\(B\left(x\right)=10x^3+3-x^4-4x^3+4x-2x^2\)

\(=-x^4+\left(10x^3-4x^3\right)-2x^2+4x+3\)

\(=-x^4+6x^3-2x^2+4x+3\)

b: M(x)=A(x)+B(x)

\(=x^4-6x^3+2x^2-x+3-x^4+6x^3-2x^2+4x+3\)

=3x+6

N(x)=A(x)-B(x)

\(=x^4-6x^3+2x^2-x+3+x^4-6x^3+2x^2-4x-3\)

\(=2x^4-12x^3+4x^2-5x\)

c: M(x)=0

=>3x+6=0

=>3x=-6

=>x=-2

Bài 3: 

a: \(A\left(x\right)=x-5x^3-2x^2+9x^3-\left(x-1\right)-2x^2\)

\(=\left(-5x^3+9x^3\right)+\left(-2x^2-2x^2\right)+\left(x-x\right)+1\)

\(=4x^3-4x^2+1\)

\(B\left(x\right)=-4x^3-2\left(x^2+1\right)+6x+2x^2-9x+2x^3\)

\(=\left(-4x^3+2x^3\right)+\left(-2x^2+2x^2\right)+6x-9x-2\)

\(=-2x^3-3x-2\)

\(C\left(x\right)=2x-6x^2-4+x^3\)

\(=x^3-6x^2+2x-4\)

b: M(x)=A(x)+B(x)-C(x)

\(=4x^3-4x^2+1-2x^3-3x-2-x^3+6x^2-2x+4\)

\(=x^3+2x^2-5x+3\)

c: \(P\left(x\right)=3\cdot M\left(x\right)-3x^3-9\)

\(=3x^3+6x^2-15x+9-3x^3-9=6x^2-15x\)

Đặt P(x)=0

=>\(6x^2-15x=0\)

=>\(2x^2-5x=0\)

=>x(2x-5)=0

=>\(\left[{}\begin{matrix}x=0\\x=\dfrac{5}{2}\end{matrix}\right.\)

Câu 3: 

a: Xét ΔACE vuông tại A và ΔKCE vuông tại K có

CE chung

\(\widehat{ACE}=\widehat{KCE}\)

Do đó: ΔACE=ΔKCE

=>CA=CK và EA=EK

Ta có: CA=CK

=>C nằm trên đường trung trực của AK(1)

Ta có: EA=EK

=>E nằm trên đường trung trực của AK(2)

Từ (1),(2) suy ra CE là đường trung trực của AK

=>CE\(\perp\)AK

b: Xét ΔABC vuông tại A có \(cosACB=\dfrac{AC}{BC}\)

=>\(\dfrac{AC}{BC}=cos60=\dfrac{1}{2}\)

=>BC=2AC

Xét ΔABC vuông tại A có \(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ABC}=90^0-60^0=30^0\)

CE là phân giác của góc ACB

=>\(\widehat{ACE}=\widehat{BCE}=\dfrac{\widehat{ACB}}{2}=30^0\)

Xét ΔEBC có \(\widehat{EBC}=\widehat{ECB}\left(=30^0\right)\)

nên ΔEBC cân tại E

=>EB=EC

mà EC>AC(ΔEAC vuông tại A)

nên EB>AC

c: Gọi H là giao điểm của BD với CA

Xét ΔCHB có

CD,BA là các đường cao

CD cắt BA tại E

Do đó: E là trực tâm của ΔCHB

=>HE\(\perp\)CB

mà EK\(\perp\)CB

nên H,E,K thẳng hàng

=>CA,EK,BD đồng quy

Bài 4:

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔBAD=ΔBED

=>BA=BE

b: Xét ΔABC có AB<AC

mà \(\widehat{ACB};\widehat{ABC}\) lần lượt là góc đối diện của các cạnh AB,AC

nên \(\widehat{ACB}< \widehat{ABC}\)

mà \(\widehat{ACB}=\widehat{AMD}\left(=90^0-\widehat{ABC}\right);\widehat{ABC}=\widehat{ADM}\left(=90^0-\widehat{BME}\right)\)

nên \(\widehat{AMD}< \widehat{ADM}< \widehat{DAM}\)

=>AD<AM<DM

c: Xét ΔDAM vuông tại A và ΔDEC vuông tại E có

DA=DE

\(\widehat{ADM}=\widehat{EDC}\)(hai góc đối đỉnh)

Do đó: ΔDAM=ΔDEC

=>DM=DC

=>D nằm trên đường trung trực của MC(1)

ta có: BA+AM=BM

BE+EC=BC

mà BA=BE và AM=EC(ΔDAM=ΔDEC)

nên BM=BC

=>B nằm trên đường trung trực của MC(2)

Ta có: KM=KC

=>K nằm trên đường trung trực của MC(3)

từ (1),(2),(3) suy ra B,D,K thẳng hàng

a: \(f\left(x\right)⋮g\left(x\right)\)

=>\(2x^2-x+2⋮x+1\)

=>\(2x^2+2x-3x-3+5⋮x+1\)

=>\(5⋮x+1\)

=>\(x+1\in\left\{1;-1;5;-5\right\}\)

=>\(x\in\left\{0;-2;4;-6\right\}\)

b: \(f\left(x\right)⋮g\left(x\right)\)

=>\(3x^2-4x+6⋮3x-1\)

=>\(3x^2-x-3x+1+5⋮3x-1\)

=>\(5⋮3x-1\)

=>\(3x-1\in\left\{1;-1;5;-5\right\}\)

=>\(3x\in\left\{2;0;6;-4\right\}\)

=>\(x\in\left\{\dfrac{2}{3};0;2;-\dfrac{4}{3}\right\}\)

mà x nguyên

nên \(x\in\left\{0;2\right\}\)

c: \(f\left(x\right)⋮g\left(x\right)\)

=>\(-2x^3-7x^2-5x+5⋮x+2\)

=>\(-2x^3-4x^2-3x^2-6x+x+2+3⋮x+2\)

=>\(3⋮x+2\)

=>\(x+2\in\left\{1;-1;3;-3\right\}\)

=>\(x\in\left\{-1;-3;1;-5\right\}\)