giúp tui vs đang cần gấp pls

<3

Gọi \(x\) (năm) là số năm nữa để tuổi con bằng \(\dfrac{5}{11}\) tuổi mẹ 

ĐK: \(x\in N,x>0\) 

Khi đó thì số tuổi con là: \(14+x\) (tuổi)

                số tuổi mẹ là: \(38+x\) (tuổi)

Mà tuổi con khi đó bằng \(\dfrac{5}{11}\) tuổi mẹ nên ta có phương trình:

\(x+14=\dfrac{5}{11}\left(x+38\right)\)

\(\Leftrightarrow x+14=\dfrac{5}{11}x+\dfrac{190}{11}\)

\(\Leftrightarrow x-\dfrac{5}{11}x=\dfrac{190}{11}-14\)

\(\Leftrightarrow\dfrac{6}{11}x=\dfrac{36}{11}\)

\(\Leftrightarrow x=\dfrac{36}{11}:\dfrac{6}{11}=6\) (năm)

Vậy: ... 

CM: Đặt số lớn là \(a\), số bé là \(b\), tổng hai số là \(c\), hiệu hai số là \(d\)\((a,b,c,d\in\mathbb{R};a>b)\)

Khi đó, ta có hệ phương trình:

\(\left\{{}\begin{matrix}a+b=c\\a-b=d\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\left(a+b\right)+\left(a-b\right)=c+d\\\left(a+b\right)-\left(a-b\right)=c-d\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2a=c+d\\2b=c-d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\left(c+d\right):2\\b=\left(c-d\right):2\end{matrix}\right.\left(\text{đpcm}\right)\)

Vậy ta có điều phải chứng minh.

Bây giờ e đang học lớp 4 =<

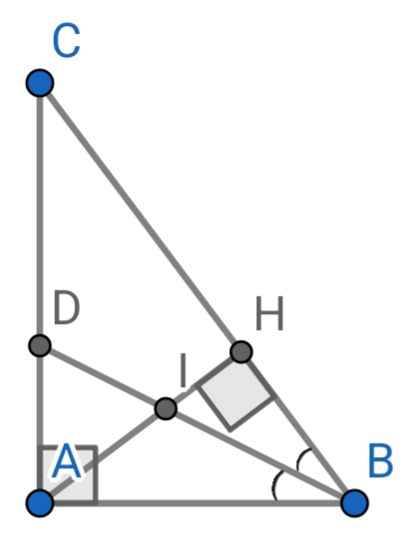
a) Do BD là đường phân giác của ∆ABC

⇒ ∠ABD = ∠CBD

⇒ ∠ABD = ∠HBI

Xét hai tam giác vuông: ∆ABD và ∆HBI có:

∠ABD = ∠HBI (cmt)

⇒ ∆ABD ∽ ∆HBI (g-g)

b) Do ∆ABD vuông tại A

⇒ ∠ADB + ∠ABD = 90⁰

⇒ ∠ADI + ∠ABD = 90⁰

Mà ∠ABD = ∠HBI (cmt)

⇒ ∠ADI + ∠HBI = 90⁰ (1)

∆HBI vuông tại H

⇒ ∠HBI + ∠HIB = 90⁰

Mà ∠HIB = ∠AID (đối đỉnh)

⇒ ∠HBI + ∠AID = 90⁰ (2)

Từ (1) và (2) ⇒ ∠ADI = ∠AID

∆ADI có:

∠ADI = ∠AID (cmt)

⇒ ∆ADI cân tại A

Đề cho $a,b,c$ nhưng tính biểu thức chứa $x,y,z$. Bạn xem lại nhé.

Ta có \(VT=\dfrac{\dfrac{4x^2}{y^2}}{\left(\dfrac{x^2}{y^2}+1\right)^2}+\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\)

Đặt \(\dfrac{x^2}{y^2}=t\left(t>0\right)\) thì VT thành

\(\dfrac{4t}{\left(t+1\right)^2}+t+\dfrac{1}{t}\)

\(=\dfrac{4t}{\left(t+1\right)^2}+\dfrac{t^2+1}{t}\)

\(=\dfrac{4t}{\left(t+1\right)^2}+\dfrac{\left(t+1\right)^2}{t}-2\)

Đặt \(\dfrac{\left(t+1\right)^2}{t}=u\left(u\ge4\right)\) (vì BĐT \(\left(a+b\right)^2\ge4ab\))

Khi đó \(VT=u+\dfrac{4}{u}-2\)

 \(=\dfrac{4}{u}+\dfrac{u}{4}+\dfrac{3u}{4}-2\)

\(\ge2\sqrt{\dfrac{4}{u}.\dfrac{u}{4}}+\dfrac{3.4}{4}-2\)

\(=2+3-2\)

\(=3\)

\(\Rightarrow VT\ge3\)

Dấu "=" xảy ra \(\Leftrightarrow u=4\) \(\Leftrightarrow t=1\) \(\Leftrightarrow x=\pm y\)

Vậy ta có đpcm. Dấu "=" xảy ra \(\Leftrightarrow x=\pm y\)

câu a

\(\dfrac{3x+15}{x^2-9}+\dfrac{1}{x+3}-\dfrac{2}{x-3}\\ =\dfrac{3\cdot\left(x+5\right)}{\left(x-3\right)\cdot\left(x+3\right)}+\dfrac{1}{x+3}-\dfrac{2}{x-3}\\ =\dfrac{3\cdot\left(x+5\right)}{\left(x-3\right)\cdot\left(x+3\right)}+\dfrac{x-3}{\left(x+3\right)\cdot\left(x-3\right)}-\dfrac{2\cdot\left(x+3\right)}{\left(x-3\right)\cdot\left(x+3\right)}\)\(=\dfrac{3\cdot\left(x+5\right)+x-3-2\cdot\left(x+3\right)}{\left(x-3\right)\cdot\left(x+3\right)}\\ =\dfrac{3x+15+x-3-2x-6}{\left(x-3\right)\cdot\left(x+3\right)}\\ =\dfrac{2x+6}{\left(x+3\right)\cdot\left(x-3\right)}\\ =\dfrac{2\cdot\left(x+3\right)}{\left(x+3\right)\cdot\left(x-3\right)}\\ =\dfrac{2}{x-3}\)

câu b

để \(\dfrac{2}{x-3}=\dfrac{2}{3}\) thì \(x-3=3\)

\(\Rightarrow x=3+3=6\)

vậy  \(x=6\) thì \(A=\dfrac{2}{3}\)