K
Khách
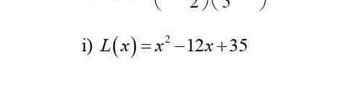
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
20 tháng 4
a: A(x)+B(x)
\(=x^3-3x^2+3x-1+2x^3+x^2-x+5\)
\(=3x^3-2x^2+2x+4\)
b: A(x)*C(x)
\(=\left(x^3-3x^2+3x-1\right)\left(x-2\right)\)
\(=x^4-2x^3-3x^3+6x^2+3x^2-6x-x+2\)
\(=x^4-5x^3+9x^2-7x+2\)
T
20 tháng 4
a) \(\dfrac{5}{3}=\dfrac{x}{9}\)
\(\Rightarrow x=\dfrac{5}{3}\cdot9\)
\(\Rightarrow x=15\)
Vậy x = 15.
b) Gọi số sách của hai lớp 7A và 7B lần lượt là \(a\), \(b\) (sách; \(a,b\in\mathbb{N}^*\))
Vì số sách của hai lớp 7A và 7B tỉ lệ thuận với số học sinh của mỗi lớp, mà số học sinh hai lớp lần lượt là 32 và 36 nên: \(\dfrac{a}{32}=\dfrac{b}{36}\)
Vì lớp 7A quyên góp được ít hơn lớp 7B 8 quyển sách nên: \(b-a=8\) (1)
Áp dụng tính chất của dãy tỉ số bằng nhau và (1), ta được:
\(\dfrac{a}{32}=\dfrac{b}{36}=\dfrac{b-a}{36-32}=\dfrac{8}{4}=2\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\cdot32=64\left(tm\right)\\b=2\cdot36=72\left(tm\right)\end{matrix}\right.\)
Vậy lớp 7A và lớp 7B quyên góp được số sách lần lượt là 64 quyển sách và 72 quyển sách.
\(Toru\)
20 tháng 4
a: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMEC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE
20 tháng 4
ΔABC cân tại A
mà AD là đường trung tuyến
nên AD\(\perp\)BC
ΔADB vuông tại D
=>\(DA^2+DB^2=AB^2\)
ΔADB vuông tại D có DE là đường cao
nên \(S_{ADB}=\dfrac{1}{2}\cdot DA\cdot DB=\dfrac{1}{2}\cdot DE\cdot AB\)
=>\(DA\cdot DB=DE\cdot AB\)
\(\left(DE+AB\right)^2-\left(DA+DB\right)^2\)
\(=DE^2+AB^2+2\cdot DE\cdot AB-DA^2-DB^2-2\cdot DA\cdot DB\)
\(=DE^2+AB^2-AD^2-BD^2+2\cdot DE\cdot AB-2\cdot DE\cdot AB\)
\(=DE^2>0\)
=>\(\left(DE+AB\right)^2>\left(DA+DB\right)^2\)
=>DE+AB>DA+DB
KV
20 tháng 4
Cho L(x) = 0
x² - 12x + 35 = 0
x² - 5x - 7x + 35 = 0
(x² - 5x) - (7x - 35) = 0
x(x - 5) - 7(x - 5) = 0
(x - 5)(x - 7) = 0
x - 5 = 0 hoặc x - 7 = 0
*) x - 5 = 0
x = 5
*) x - 7 = 0
x = 7
Vậy nghiệm của đa thức L(x) là: x = 5; x = 7
20 tháng 4
a:
ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là phân giác của góc BAC và AD\(\perp\)BC
Xét ΔABC có
AD,BE là các đường cao
AD cắt BE tại H
Do đó: H là trực tâm của ΔABC
=>CH\(\perp\)AB
b: Xét ΔIBC có
BA là đường trung tuyến
\(BA=\dfrac{IC}{2}\)
Do đó; ΔIBC vuông tại B
Xét tứ giác BDAK có
\(\widehat{BDA}=\widehat{BKA}=\widehat{KBD}=90^0\)
=>BDAK là hình chữ nhật
=>\(\widehat{KAD}=90^0\)
c: BDAK là hình chữ nhật
=>AB=DK
BDAK là hình chữ nhật
=>BA cắt DK tại trung điểm của mỗi đường
=>J là trung điểm chung của BA và DK
d: Xét ΔOAL và ΔOCB có
OA=OC
\(\widehat{AOL}=\widehat{COB}\)(hai góc đối đỉnh)
OL=OB
Do đó: ΔOAL=ΔOCB
=>\(\widehat{OAL}=\widehat{OCB}\)
=>AL//CB
mà KA//BC
nên A,L,K thẳng hàng
20 tháng 4
a: Xét ΔCED vuông tại E và ΔCFD vuông tại F có
CD chung
\(\widehat{ECD}=\widehat{FCD}\)
Do đó: ΔCED=ΔCFD
=>CE=CF: DE=DF
Xét ΔCEK vuông tại E và ΔCFH vuông tại F có
CE=CF
\(\widehat{ECK}\) chung
Do đó: ΔCEK=ΔCFH
b: Xét ΔDEH vuông tại E và ΔDFK vuông tại F có
DE=DF
\(\widehat{EDH}=\widehat{FDK}\)
Do đó: ΔDEH=ΔDFK
=>DH=DK
=>D nằm trên đường trung trực của HK(1)
Ta có: CH=CK
=>C nằm trên đường trung trực của HK(2)
Ta có: MH=MK
=>M nằm trên đường trung trực của HK(3)
Từ (1),(2),(3) suy ra C,D,M thẳng hàng