
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :
3 × x - 10 = 2 × x + 13
=> 2 × x + 13 + 10 = 3 × x
Vậy x = 10 + 13 = 23
Tick cho mình nha

Lời giải:
$a^3+3a^2+5=5^b$
$\Rightarrow a^2(a+3)+5=5^b$
$\Rightarrow a^2.5^c+5=5^b$
$\Rightarrow 5(a^2.5^{c-1}+1-5^{b-1})=0$
$\Rightarrow a^2.5^{c-1}+1=5^{b-1}$
Nếu $b,c$ đều là số nguyên dương lớn hơn $1$ thì:
$1=5^{b-1}-a^2.5^{c-1}\vdots 5$ (vô lý)
Do đó trong 2 số $b,c$ tồn tại ít nhất 1 số nguyên dương bằng 1
Nếu $b=1$ thì:
$a^2.5^{c-1}+1=5^{1-1}=1\Rightarrow a^2.5^{c-1}=0$
$\Rightarrow a=0$ (không tm do $a$ nguyên dương)
Nếu $c=1$ thì $a+3=5^c=5\Rightarrow a=2$
$a^2.5^{c-1}+1=5^{b-1}$
$\Leftrightarrow a^2.5^{1-1}+1=5^{b-1}$
$\Leftrightarrow 2^2+1=5^{b-1}\Rightarrow b-1=1\Rightarrow b=2$
Vậy $(a,b,c)=(2,2,1)$

Gọi số cây lớp 7A,7B,7C trồng được lần lượt là a(cây),b(cây),c(cây)
(Điều kiện: \(a,b,c\in Z^+\))
Số cây lớp 7A;7B;7C trồng được lần lượt tỉ lệ thuận với 9;8;7
=>\(\dfrac{a}{9}=\dfrac{b}{8}=\dfrac{c}{7}\)
Lớp 7C trồng ít hơn lớp 7A 10 cây nên ta có: a-c=10
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{9}=\dfrac{b}{8}=\dfrac{c}{7}=\dfrac{a-c}{9-7}=\dfrac{10}{2}=5\)
=>\(a=5\cdot9=45;b=5\cdot8=40;c=5\cdot7=35\)
Vậy: số cây lớp 7A,7B,7C trồng được lần lượt là 45 cây; 40 cây; 35 cây

a: \(3x^3+ax^2+bx+9⋮x^2-9\)
=>\(3x^3-27x+ax^2-9a+\left(b+27\right)x+9a+9⋮x^2-9\)
=>\(\left\{{}\begin{matrix}b+27=0\\9a+9=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=-27\\a=-1\end{matrix}\right.\)
b: \(10n^2+n-10⋮n-1\)
=>\(10n^2-10n+11n-11+1⋮n-1\)
=>\(1⋮n-1\)
=>\(n-1\in\left\{1;-1\right\}\)
=>\(n\in\left\{2;0\right\}\)

a: M là trung điểm của BC
=>\(BM=CM=\dfrac{BC}{2}\)
mà BA=BC/2
nên BM=CM=BA
Xét ΔBAD và ΔBMD có
BA=BM
\(\widehat{ABD}=\widehat{MBD}\)
BD chung
Do đó: ΔBAD=ΔBMD
b: ta có; ΔBAD=ΔBMD
=>\(\widehat{BAD}=\widehat{BMD}\)
Xét ΔBAC và ΔBME có
\(\widehat{BAC}=\widehat{BME}\)
BA=BM
\(\widehat{ABC}\) chung
Do đó: ΔBAC=ΔBME
=>BE=BC
=>ΔBEC cân tại B
Ta có: ΔBEC cân tại B
mà BD là đường phân giác
nên DB là đường trung tuyến
=>N là trung điểm của EC
Xét ΔEBC có
BN,EM là các đường trung tuyến
BN cắt EM tại D
Do đó: D là trọng tâm của ΔEBC
=>BD/DN=2

Đồ thị hàm số đi qua A(- \(\dfrac{1}{2}\); 1)
⇔ m.|- \(\dfrac{1}{2}\)| + 2.(-\(\dfrac{1}{2}\)) = 1
\(\dfrac{1}{2}\)m - 1 = 1
\(\dfrac{1}{2}\)m = 2
m = 2 x 2
m = 4
Kết luận với m = 4 thì đồ thị hàm số đi qua A(- \(\dfrac{1}{2}\); 1)

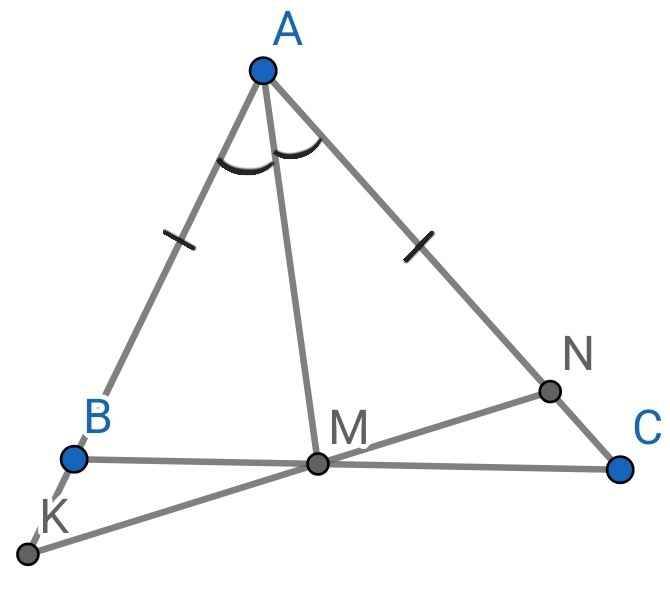
Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
⇒ ∠BAM = ∠NAM
Xét ∆ABM và ∆ANM có:
AB = AN (gt)
∠BAM = ∠NAM (cmt)
AM là cạnh chung
⇒ ∆ABM = ∆ANM (c-g-c)
⇒ MB = MN (hai cạnh tương ứng)

Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)=180^0-65^0=115^0\)
=>\(\widehat{IBC}+\widehat{ICB}=57,5^0\)
Xét ΔIBC có \(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^0\)
=>\(\widehat{BIC}=180^0-57,5^0=122,5^0\)



Câu 1:
$f(x)=(2x^4-x^4)-6x^3+(3x^2-x^2)-x+1$
$=x^4+2x^2-x+1$
Bậc của $f(x)$: $4$
Hệ số cao nhất của $f(x)$: $1$
Hệ số tự do của $f(x)$: $1$
-----------------
$g(x)=2x^3-x+x^2+x^3=(2x^3+x^3)+x^2-x$
$=3x^3+x^2-x$
Bậc của $g(x)$: $3$
Hệ số cao nhất của $g(x)$: $3$
Hệ số tự do của $g(x)$: $0$
2
$f(x)=h(x)+g(x)$
$h(x)=f(x)-g(x)=(x^4+2x^2-x+1)-(3x^3+x^2-x)$
$=x^4+2x^2-x+1-3x^3-x^2+x$
$=x^4-3x^3+(2x^2-x^2)+(-x+x)-1=x^4-3x^3+x^2-1$
Câu 2:
1.
$A(x)=2(-x+5)-\frac{3}{2}(x-4)=-2x+10-\frac{3}{2}x+6$
$=-\frac{7}{2}x+16=0$
$\Rightarrow \frac{-7}{2}x=-16$
$\Rightarrow x=(-16): \frac{-7}{2}=\frac{32}{7}$
Vậy $x=\frac{32}{7}$ là nghiệm của $A(x)$
2.
$B(x)=-4x^2+9=0$
$\Rightarrow 4x^2=9$
$\Rightarrow (2x)^2=9=3^2=(-3)^2$
$\Rightarrow 2x=3$ hoặc $2x=-3$
$\Rightarrow x=\frac{3}{2}$ hoặc $x=\frac{-3}{2}$
Vậy $B(x)$ có nghiệm $x=\pm \frac{3}{2}$
3.
$C(x)=x^3+4x=x(x^2+4)=0$
$\Rightarrow x=0$ hoặc $x^2+4=0$
$\Rightarrow x=0$ hoặc $x^2=-4<0$ (vô lý)
Vậy $x=0$ là nghiệm của $C(x)$