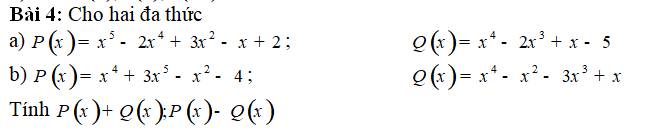
giúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




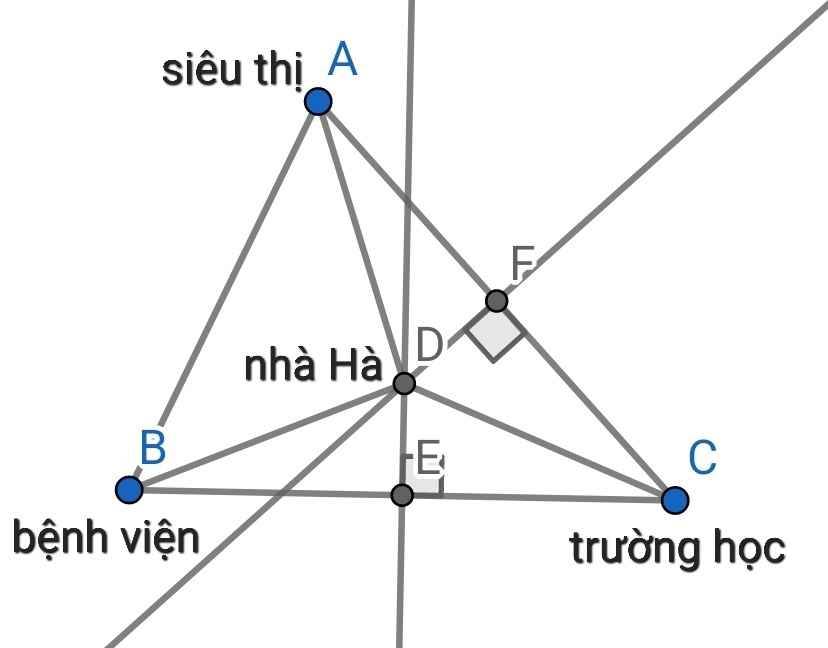
Để khoảng cách từ vị trí của nhà Hà đến siêu thị, bệnh viện, trường học đều bằng nhau thì nhà Hà nằm ở vị trí D là giao điểm của ba đường trung trực của ∆ABC như hình vẽ.
Siêu thị, bệnh viện, trường học nằm ở ba vị trí là ba đỉnh của ∆ABC

1) 1/2 x³.(4x² - 5x + 7)
= 2x⁵ - 5x⁴/2 + 7x³/2
b) (8x³ - 1) : (4x² + 2x + 1)
= (2x - 1)(4x² + 2x + 1) : (4x² + 2x + 1)
= 2x - 1
c) (2x - 4)(2x + 4)
= (2x)² - 4²
= 4x² - 16
d) (25y³ - 20y⁴ + 7y²) : (-5y²)
= -5y + 4y² - 7/5

Lời giải:
b.
$(x-1)(x+2)-(x+1)(x-3)-3x=1$
$\Leftrightarrow (x^2+x-2)-(x^2-2x-3)-3x=1$
$\Leftrightarrow x^2+x-2-x^2+2x+3-3x=1$
$\Leftrightarrow 0=0$ (luôn đúng)
Vậy PT có nghiệm $x$ là số thực bất kỳ
c.
$(3x+7)(2x+3)-(3x-5)(2x+11)=0$
$\Leftrightarrow (6x^2+23x+21)-(6x^2+23x-55)=0$
$\Leftrightarrow 76=0$ (vô lý)
Vậy không tồn tại $x$ thỏa mãn đề.
a) \(P\left(x\right)=x^5-2x^4+3x^2-x+2;Q\left(x\right)=x^4-2x^3+x-5\)
+, \(P\left(x\right)+Q\left(x\right)=\left(x^5-2x^4+3x^2-x+2\right)+\left(x^4-2x^3+x-5\right)\)
\(=x^5-2x^4+3x^2-x+2+x^4-2x^3+x-5\)
\(=x^5+\left(-2x^4+x^4\right)-2x^3+3x^2+\left(-x+x\right)+\left(2-5\right)\)
\(=x^5-x^4-2x^3+3x^2-3\)
+, \(P\left(x\right)-Q\left(x\right)=\left(x^5-2x^4+3x^2-x+2\right)-\left(x^4-2x^3+x-5\right)\)
\(=x^5-2x^4+3x^2-x+2-x^4+2x^3-x+5\)
\(=x^5+\left(-2x^4-x^4\right)+2x^3+3x^2+\left(-x-x\right)+\left(2+5\right)\)
\(=x^5-3x^4+2x^3+3x^2-2x+7\)
b) \(P\left(x\right)=x^4+3x^5-x^2-4;Q\left(x\right)=x^4-x^2-3x^3+x\)
+, \(P\left(x\right)+Q\left(x\right)=\left(x^4+3x^5-x^2-4\right)+\left(x^4-x^2-3x^3+x\right)\)
\(=x^4+3x^5-x^2-4+x^4-x^2-3x^3+x\)
\(=3x^5+\left(x^4+x^4\right)-3x^3+\left(-x^2-x^2\right)+x-4\)
\(=3x^5+2x^4-3x^3-2x^2+x-4\)
+, \(P\left(x\right)-Q\left(x\right)=\left(x^4+3x^5-x^2-4\right)-\left(x^4-x^2-3x^3+x\right)\)
\(=x^4+3x^5-x^2-4-x^4+x^2+3x^3-x\)
\(=3x^5+\left(x^4-x^4\right)+3x^3+\left(-x^2+x^2\right)-x-4\)
\(=3x^5+3x^3-x-4\)
\(\text{#}Toru\)