Câu 4: Một khối có 50 học sinh đi thi học sinh giỏi và đều đạt giải. Trong đó số học sinh đạt giải nhất chiếm 12 tổng số học sinh; số học sinh đạt giải nhì bằng 80% số học sinh đạt giải nhất; còn lại là học sinh đạt giải ba. Tính số học sinh đạt giải ba của khối.
Câu 12: Lớp 6A có 40 học sinh được xếp thành ba loại: học sinh giỏi, học sinh tiên tiến và học sinh trung bình. Số học sinh giỏi chiếm 14 số học sinh cả lớp.
a) Tính số học sinh giỏi của lớp 6A.
b) Biết 25 số học sinh tiên tiến của lớp 6A là 8 bạn. Tính số học sinh tiên tiến.
c) Tính tỉ số phần trăm của số học sinh trung bình so với tổng số học sinh của lớp 6A

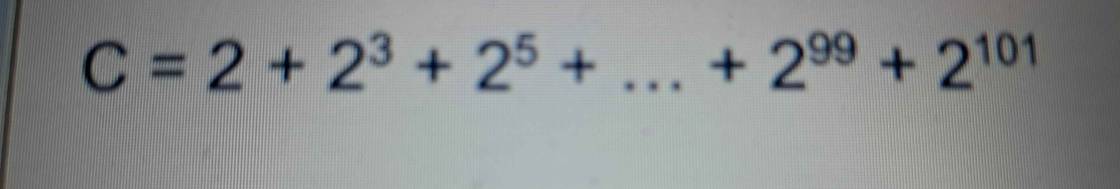

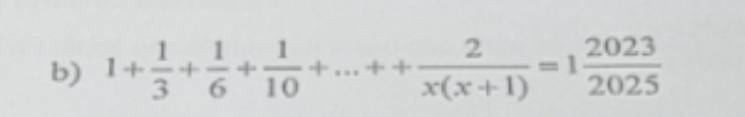
Em ghi đề cho chính xác lại số liệu