Lời giải:

$x^2-7x-8=0$

$\Leftrightarrow (x^2+x)-(8x+8)=0$

$\Leftrightarrow x(x+1)-8(x+1)=0$

$\Leftrightarrow (x+1)(x-8)=0$

$\Rightarrow x+1=0$ hoặc $x-8=0$

$\Rightarrow x=-1$ hoặc $x=8$

7a/

$x^3y+x-y-1=(x^3y-y)+(x-1)=y(x^3-1)+(x-1)$

$=y(x-1)(x^2+x+1)+(x-1)=(x-1)[y(x^2+x+1)+1]$

$=(x-1)(x^2y+xy+y+1)$

7b/

$x^2(x-2)+4(2-x)=x^2(x-2)-4(x-2)=(x-2)(x^2-4)$

$=(x-2)(x-2)(x+2)=(x-2)^2(x+2)$
7c/

$x^3-x^2-20x=x(x^2-x-20)=x[(x^2+4x)-(5x+20)]$

$x[x(x+4)-5(x+4)]=x(x+4)(x-5)$

7d/

$(x^2+1)^2-(x+1)^2=[(x^2+1)-(x+1)][(x^2+1)+(x+1)]$

$=(x^2-x)(x^2+x+2)$

$=x(x-1)(x^2+x+2)$

7e/

$6x^2-7x+2=(6x^2-3x)-(4x-2)=3x(2x-1)-2(2x-1)=(2x-1)(3x-2)$

7f/

$x^4+8x^2+12=(x^4+6x^2)+(2x^2+12)=x^2(x^2+6)+2(x^2+6)$

$=(x^2+6)(x^2+2)$

7g/

$(x^3+x+1)(x^3+x)-2=(t+1)t-2$ (đặt $x^3+x=t$)

$=t^2+t-2=(t^2+2t)-(t+2)=t(t+2)-(t+2)$

$=(t+2)(t-1)=(x^3+x+2)(x^3+x-1)$

$=[(x^3+x^2)-(x^2+x)+(2x+2)](x^3+x-1)$

$=[x^2(x+1)-x(x+1)+2(x+1)](x^3+x-1)$

$=(x+1)(x^2-x+2)(x^3+x-1)$

chịu :))
 

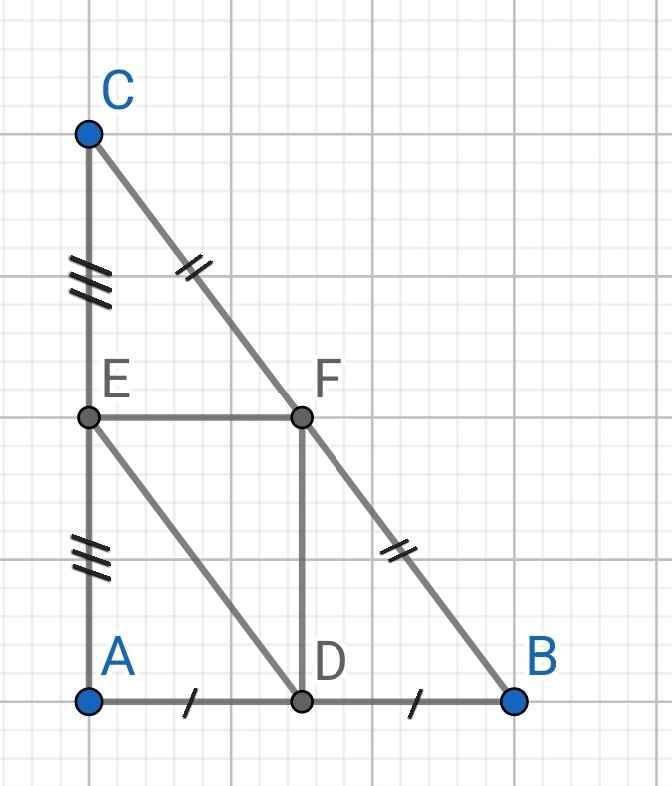 a) Ta có:

BC² = 25² = 625

AB² + AC² = 15² + 20²

= 225 + 400

= 625

⇒ BC² = AB² + AC² (= 625)

Theo định lý Pytago đảo

⇒ ∆ABC vuông tại A

Do D là trung điểm của AB (gt)

E là trung điểm của AC (gt)

⇒ DE là đường trung bình của ∆ABC

⇒ DE = BC : 2

= 25 : 2

= 12,5 (cm)

Do E là trung điểm của AC (gt)

F là trung điểm của BC (gt)

⇒ EF là đường trung bình của ∆ABC

⇒ EF = AB : 2

= 15 : 2 

= 7,5 (cm)

Do D là trung điểm của AB (gt)

F là trung điểm của AC (gt)

⇒ DF là đường trung bình của ∆ABC

⇒ DF = AC : 2

= 20 : 2

= 10 (cm)

b) Ta có:

EF² + DF² = 7,5² + 10² = 156,25

DE² = 12,5² = 156,25

⇒ DE² = EF² + DF² (= 156,25)

Theo định lý Pytago đảo

⇒ ∆DEF vuông tại F

2xy - 4x + 5y - 10

= (2xy - 4x) + (5y - 10)

= 2x(y - 2) + 5(y - 2)

= (y - 2)(2x + 5)

2xy - 4x + 5y -10

= 2x(y-2) + 5(y-2)

= (2x+5)(y-2)

Trả lời 

Lời giải:

$x^2-6x+3=4y^2$

$\Leftrightarrow (x^2-6x+9)-6=4y^2$

$\Leftrightarrow (x-3)^2-6=4y^2$
$\Leftrightarrow 6=(x-3)^2-4y^2=(x-3)^2-(2y)^2=(x-3-2y)(x-3+2y)$

Ta thấy: $x-3-2y+(x-3+2y)=2(x-3)$ chẵn nên $x-3-2y, x-3+2y$ có cùng tính chẵn lẻ.

Mà tích $(x-3-2y)(x-3+2y)=6=1.6=6.1=2.3=3.2$ đều là các thừa số khác tính chẵn lẻ

$\Rightarrow$ không tồn tại $x,y$ nguyên thỏa mãn đề.