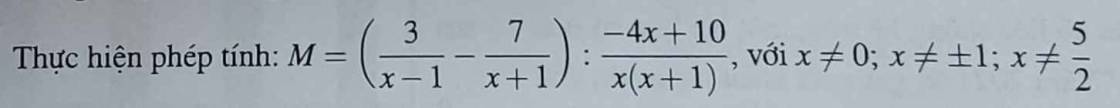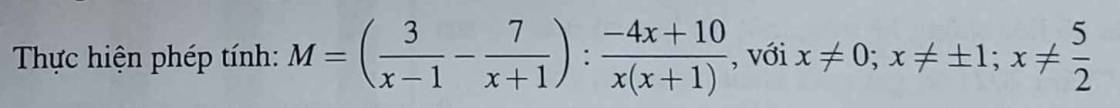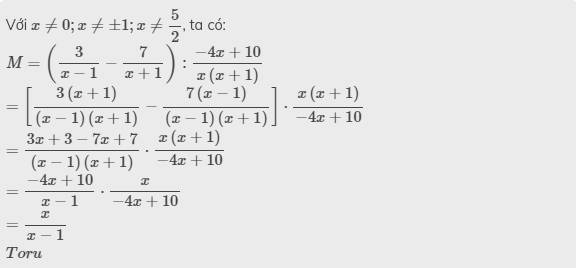Khi nào thi sử dụng biểu đồ tranh?
Nêu ưu điểm khi sử dụng biểu đồ tranh.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. Xét tam giác $AME$ và $AHE$ có:
$AE$ chung
$\widehat{AEM}=\widehat{AEH}=90^0$
$ME=HE$ (gt)
$\Rightarrow \triangle AME=\triangle AHE$(c.g.c)
$\Rightarrow AM=AH(1)$
Hoàn toàn tương tự ta có $\triangle AHF=\triangle ANF$ (c.g.c)
$\Rightarrow AH=AN(2)$
Từ $(1); (2)\Rightarrow AM=AN$ nên tam giác $AMN$ là tam giác cân tại $A$.
b.
Ta có:
$\frac{HE}{EM}=\frac{HF}{FN}=1$ nên theo định lý Talet thì $EF\parallel MN$
c.
Vì tam giác $AMN$ cân tại $A$ (cm ở phần a) nên trung tuyến $AI$ đồng thời là đường cao.
$\Rightarrow AI\perp MN$
Mà $MN\parallel EF$
$\Rightarrow AI\perp EF$ (đpcm)


x²y + xy² - x - y
= (x²y + xy²) - (x + y)
= xy(x + y) - (x + y)
= (x + y)(xy - 1)

a) Ta tính tổng số các cặp lớp phân biệt có thể xảy ra.
Vị trí đầu tiên có \(x\) cách chọn và vị trí thứ hai sẽ có \(x-1\) cách chọn (do một lớp bất kì không thể đấu với chính lớp đó). Nhưng nếu tính như trên, thì mỗi trận đấu giữa 2 đội bất kì sẽ bị lặp lại thêm 1 lần, nên tổng số trận đấu khác nhau là \(\dfrac{x\left(x-1\right)}{2}\)
b) Cho \(\dfrac{x\left(x-1\right)}{2}=105\)
\(\Leftrightarrow x^2-x-210=0\)
\(\Leftrightarrow\left(x-21\right)\left(x+20\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=21\left(nhận\right)\\x=-20\left(loại\right)\end{matrix}\right.\)
Vậy có 21 đội tham gia.

Với \(x\ne0;x\ne\pm1;x\ne\dfrac{5}{2}\), ta có:
\(M=\left(\dfrac{3}{x-1}-\dfrac{7}{x+1}\right):\dfrac{-4x+10}{x\left(x+1\right)}\)
\(=\left[\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}-\dfrac{7\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{x\left(x+1\right)}{-4x+10}\)
\(=\dfrac{3x+3-7x+7}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x\left(x+1\right)}{-4x+10}\)
\(=\dfrac{-4x+10}{x-1}\cdot\dfrac{x}{-4x+10}\)
\(=\dfrac{x}{x-1}\)
\(Toru\)

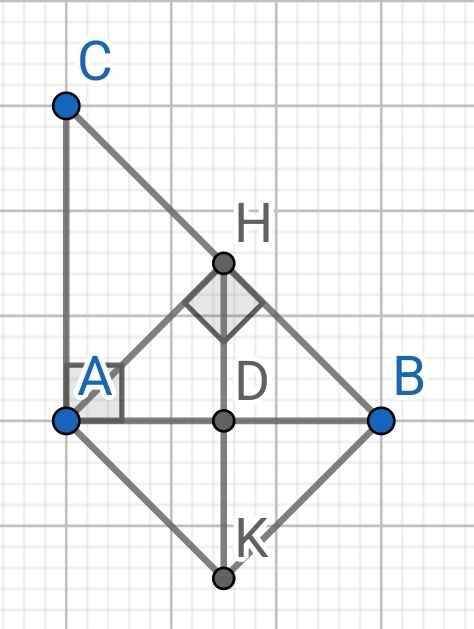
Do AH ⊥ BC (gt)
⇒ AH ⊥ BH
Do ∆ABC vuông cân tại A (gt)
AH là đường cao
⇒ AH cũng là đường trung tuyến của ∆ABC
⇒ H là trung điểm của BC
Gọi D là giao điểm của AB và HK
Do H và K đối xứng nhau qua AB (gt)
⇒ D là trung điểm của HK và AB là đường trung trực của HK
⇒ HK ⊥ AB
Mà AB ⊥ AC
⇒ HK // AC
⇒ HD // AC
Mà H là trung điểm của BC
⇒ D là trung điểm AB
Do ∆ABC vuông cân tại A (gt)
AH là đường trung tuyến của ∆ABC (cmt)
⇒ AH = HB = HC = BC : 2
Tứ giác AHBK có:
D là trung điểm HK (cmt)
D là trung điểm AB (cmt)
⇒ AHBK là hình bình hành
Mà AH ⊥ BH (cmt)
⇒ AHBK là hình chữ nhật
Lại có AH = BH (cmt)
⇒ AHBK là hình vuông

Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn.