a: \(101^2=\left(100+1\right)^2=100^2+2\cdot100\cdot1+1^2\)

=10000+200+1

=10201

b: \(64^2+36^2+72\cdot64\)

\(=64^2+2\cdot64\cdot36+36^2\)

\(=\left(64+36\right)^2=100^2=10000\)

c: \(54^2+46^2-2\cdot54\cdot46=\left(54-46\right)^2=8^2=64\)

d: \(98\cdot102=\left(100-2\right)\left(100+2\right)=100^2-4=9996\)

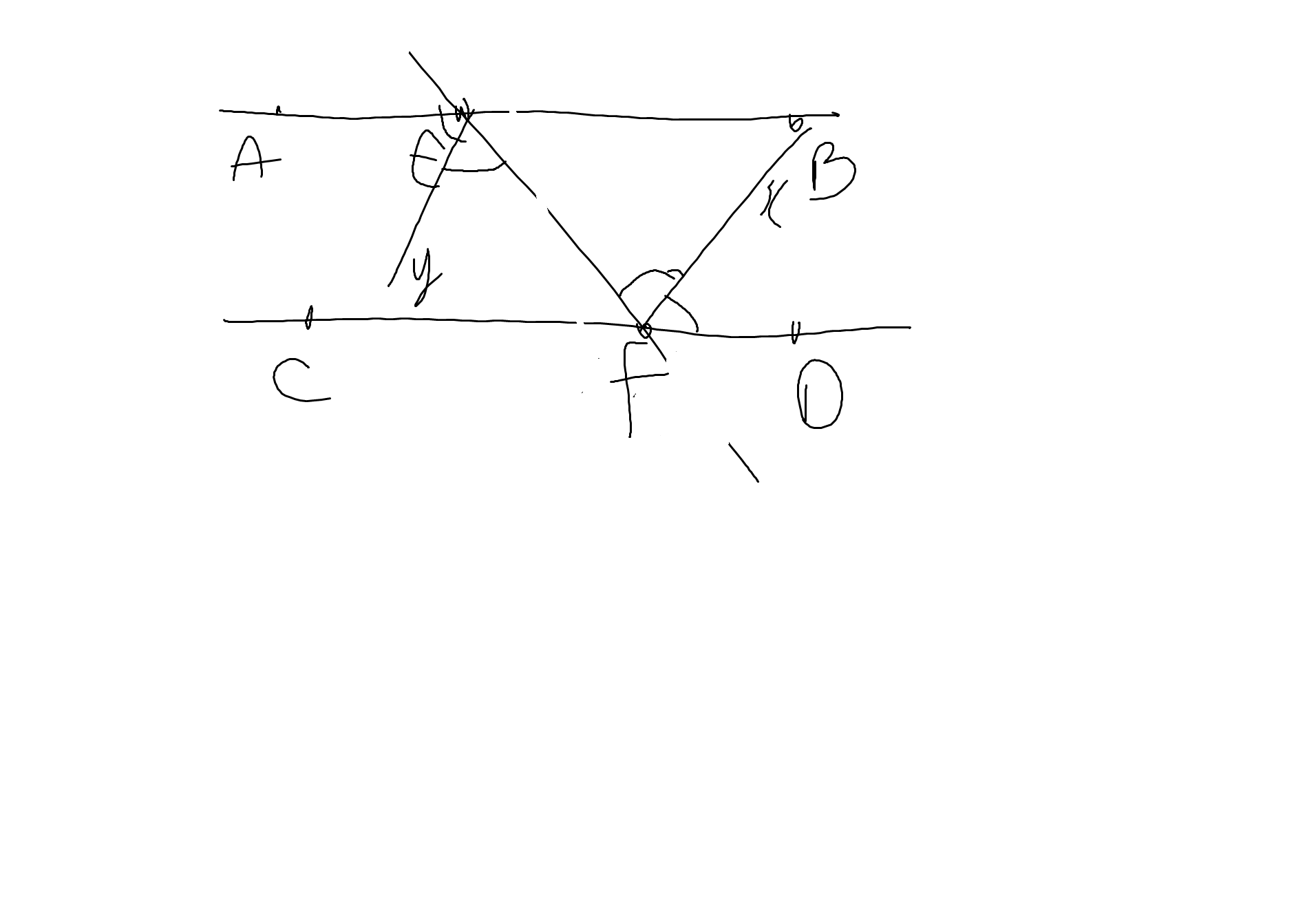
Gọi hai góc so le trong là \(\widehat{AEF};\widehat{EFD}\); Ey;Fx lần lượt là phân giác của góc AEF;góc EFD

Vì AB//CD nên \(\widehat{AEF}=\widehat{EFD}\)(hai góc so le trong)

mà \(\widehat{yEF}=\dfrac{\widehat{AEF}}{2};\widehat{xFE}=\dfrac{\widehat{EFD}}{2}\)

nên \(\widehat{yEF}=\widehat{xFE}\)

mà hai góc này là hai góc ở vị trí so le trong

nên Ey//Fx

\(x\div30\%=x\div\dfrac{3}{10}=x\times\dfrac{10}{3}\)

\(\Rightarrow\) Thay \(\dfrac{10}{3}\) vào dấu ?

\(\left(2x-3\right)^9-2x+3=0\)

=>\(\left(2x-3\right)^9-\left(2x-3\right)=0\)

=>\(\left(2x-3\right)\left[\left(2x-3\right)^8-1\right]=0\)

=>\(\left[{}\begin{matrix}2x-3=0\\\left(2x-3\right)^8-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\\left(2x-3\right)^8=1\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=\dfrac{3}{2}\\2x-3=1\\2x-3=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=2\\x=1\end{matrix}\right.\)

a<b

=>a+3<b+3

mà b+3<b+5

nên a+3<b+5

\(7\cdot4^{x-1}+4^{x+1}=4^x\cdot7\cdot\dfrac{1}{4}+4^x\cdot4\)

\(=4^x\left(7,25+4\right)=11,25\cdot4^x\)

\(50+\dfrac{50}{3}+\dfrac{25}{3}+\dfrac{20}{4}+...+\dfrac{100}{98\cdot99}+\dfrac{1}{99}\)

\(=\dfrac{100}{2}+\dfrac{100}{6}+\dfrac{100}{12}+...+\dfrac{100}{98\cdot99}+\dfrac{100}{99\cdot100}\)

\(=100\cdot\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)

\(=100\cdot\dfrac{99}{100}=99\)

\(\dfrac{1}{2\times4\times6}+\dfrac{1}{4\times6\times8}+...+\dfrac{1}{96\times98\times100}\\ =\dfrac{1}{8}\times\dfrac{1}{1\times2\times3}+\dfrac{1}{8}\times\dfrac{1}{2\times3\times4}+...+\dfrac{1}{8}\times\dfrac{1}{48\times49\times50}\\ =\dfrac{1}{8}\times\left(\dfrac{1}{1\times2\times3}+\dfrac{1}{2\times3\times4}+...+\dfrac{1}{48\times49\times50}\right)\)

Đặt \(A=\dfrac{1}{1\times2\times3}+\dfrac{1}{2\times3\times4}+...+\dfrac{1}{48\times49\times50}\)
\(2A=\dfrac{2}{1\times2\times3}+\dfrac{2}{2\times3\times4}+...+\dfrac{2}{48\times49\times50}\\ 2A=\dfrac{1}{1\times2}-\dfrac{1}{2\times3}+\dfrac{1}{2\times3}-\dfrac{1}{3\times4}+...+\dfrac{1}{48\times49}-\dfrac{1}{49\times50}\\ 2A=\dfrac{1}{1\times2}-\dfrac{1}{49\times50}\\ 2A=\dfrac{1}{2}-\dfrac{1}{2450}\\ 2A=\dfrac{612}{1225}\\ A=\dfrac{306}{1225}\)
Thay vào biểu thức ban đầu được:
\(\dfrac{1}{2\times4\times6}+\dfrac{1}{4\times6\times8}+...+\dfrac{1}{96\times98\times100}\\ =\dfrac{1}{8}\times\dfrac{306}{1225}\\ =\dfrac{153}{4900}\)

`S = 1.4+2.5 + 3.6 +...+ 100.103`

`S = 1 . (2+2) + 2 (3+2) + 3 . (4+2) + ... + 100 . (101 + 2) `

`S = 1.2 + 2 . 1 + 2.3 + 2.2 + 3.4 + 2.3 + ... + 100 . 101 + 2. 100`

`S = 1.2 + 2.3+ 3.4 +... + 100.101 + 2.1 + 2.2 + 2.3 + ... + 2.100`

`S =  1.2 + 2.3+ 3.4 +... + 100.101 + 2(1+2+3+...+100) `

`S =  1.2 + 2.3+ 3.4 +... + 100.101 + 2 (100+1) . [(100-1):1+1] : 2`

`S =  1.2 + 2.3+ 3.4 +... + 100.101 + 10100`

Đặt `A = 1.2 + 2.3+ 3.4 +... + 100.101`

`3A = 1.2.3 + 2.3.(4-1) + 3.4.(5-2) + .... + 100 . 101. (102 - 99)`

`3A = 1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+100.101.102 -99.100.101`

`3A = 100.101.102`

`A = 343400`

`S = A + 10100`

`= 343400 + 10100`

`= 353500`

5 số =1,9,2,8,0

=(1+9).(2+8)+0

.=nhân