Đồng nhất thức có áp dụng giải phương trình bậc 3 nhiều nghiệm vô tỉ và các bậc cao hơn không có thể vẽ tất cả các hình đa giác đều bằng các góc bằng nhau trong đường tròn ko liệu đường tròn có phải đa giác đều ko có thể dùng dấu hiệu nhận biết để dựng công thức không
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có \(\lim\limits_{x\rightarrow-\infty}\dfrac{4x+1}{-x+1}=\lim\limits_{x\rightarrow-\infty}\left(\dfrac{-4+\dfrac{1}{x}}{1+\dfrac{1}{x}}\right)=-4\)
b) Ta có \(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{x^2-x-2}{x-2}=\lim\limits_{x\rightarrow2}\left(\dfrac{\left(x+1\right)\left(x-2\right)}{x-2}\right)\)
\(=\lim\limits_{x\rightarrow2}\left(x+1\right)=2+1=3\)
Để hàm số đã cho liên tục tại \(x=2\) thì \(\lim\limits_{x\rightarrow2}f\left(x\right)=f\left(2\right)=m\) hay \(m=3\).


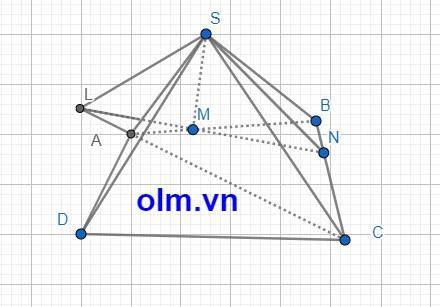
S \(\in\) (SMN) \(\cap\) (SAC) (1)
Trong mặt phẳng ABCD gọi L = AC \(\cap\) MN
Ta có: \(\left\{{}\begin{matrix}L\in MN,MN\subset\left(SMN\right)\\L\in AC,AC\subset\left(SAC\right)\end{matrix}\right.\) ⇒ L \(\in\) (SAC) \(\cap\) (SMN) (2)
Từ (1) và (2) ta có: (SAC) \(\cap\) (SMN) = SL
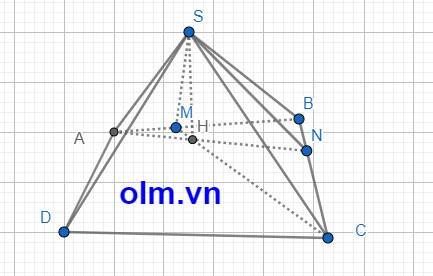
Ta có: S \(\in\) (SAN) \(\cap\) (SCM) (1)
Trong mặt phẳng ABCD gọi H = AN \(\cap\) CM
Vì: \(\left\{{}\begin{matrix}H\in AN,AN\subset\left(SAN\right)\\H\in CM,CM\subset\left(SCM\right)\end{matrix}\right.\) ⇒ H \(\in\) (SAN) \(\cap\) (SCM) (2)
Từ (1) và (2) ta có: (SAN) \(\cap\) (SCM) = SH

