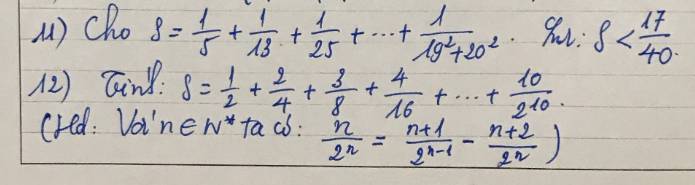
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x-1}{2}=\dfrac{2-x}{3}\)
\(\Rightarrow3\cdot\left(x-1\right)=2\cdot\left(2-x\right)\)
\(\Rightarrow3x-3=4-2x\)
\(\Rightarrow3x+2x=4+3\)
\(\Rightarrow5x=7\)
\(\Rightarrow x=\dfrac{7}{5}\)
\(x-\dfrac{1}{2}=2-\dfrac{x}{3}\)
\(x+\dfrac{x}{3}=2+\dfrac{1}{2}\)
\(x\left(1+\dfrac{1}{3}\right)=\dfrac{5}{2}\)
\(x\times\dfrac{4}{3}=\dfrac{5}{2}\)
\(x=\dfrac{5}{2}:\dfrac{4}{3}\)
\(x=\dfrac{15}{8}\)

Câu 6:
a: MB=2MC
=>\(\dfrac{CM}{CB}=\dfrac{1}{3};\dfrac{BM}{BC}=\dfrac{2}{3}\)
Ta có: BM=2/3BC
=>\(S_{MBE}=\dfrac{2}{3}\cdot S_{BEC}\)
Vì CM=1/3CB
nên \(S_{MCD}=\dfrac{1}{3}\cdot S_{BCD}\)
Xét ΔMAB và ΔMEC có
\(\widehat{MAB}=\widehat{MEC}\)(hai góc so le trong, AB//EC)
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
Do đó: ΔMAB~ΔMEC
=>\(\dfrac{AB}{EC}=\dfrac{BM}{CM}=2\)
=>\(\dfrac{CD}{CE}=2\)
=>\(S_{BCD}=2\cdot S_{BCE}\)
=>\(\dfrac{1}{3}\cdot S_{BCD}=\dfrac{2}{3}\cdot S_{BCE}\)
=>\(S_{MBE}=S_{MCD}\)
b: \(MB=\dfrac{2}{3}BC\)
mà BC=AD
nên \(\dfrac{MB}{AD}=\dfrac{2}{3}\)
Xét ΔOBM và ΔODA có
\(\widehat{OBM}=\widehat{ODA}\)(BM//DA)
\(\widehat{BOM}=\widehat{DOA}\)(hai góc đối đỉnh)
Do đó: ΔOBM~ΔODA
=>\(\dfrac{OB}{OD}=\dfrac{MB}{DA}=\dfrac{2}{3}\)

Bài 43: Sửa đề: Trên tia Ox
a: Trên tia Ox, ta có: OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB+4=7
=>AB=3(cm)
b: Vì BA và BD là hai tia đối nhau
nên B nằm giữa A và D
=>AD=AB+BD=3+1=4(cm)
c: Vì OA=AD(=4cm)
nên A là trung điểm của OD
Bài 44:
\(S=\dfrac{3^2}{1\cdot3}+\dfrac{3^2}{3\cdot5}+...+\dfrac{3^2}{2021\cdot2023}\)
\(=\dfrac{9}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2021\cdot2023}\right)\)
\(=\dfrac{9}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\right)\)
\(=\dfrac{9}{2}\left(1-\dfrac{1}{2023}\right)=\dfrac{9}{2}\cdot\dfrac{2022}{2023}=\dfrac{9099}{2023}\)

\(\dfrac{11}{19}.\dfrac{12}{29}-\dfrac{11}{19}.\dfrac{2}{29}+\dfrac{11}{19}.\dfrac{19}{29}\)
\(=\dfrac{11}{19}.\left(\dfrac{12}{29}-\dfrac{2}{29}+\dfrac{19}{29}\right)\)
\(=\dfrac{11}{19}.1\)
\(=\dfrac{11}{19}\)

3/4 giá niêm yết là:
\(\dfrac{3}{4}\cdot300000=225000\left(đồng\right)\)
Giá vốn là \(225000\cdot\dfrac{100}{125}=180000\left(đồng\right)\)
Để lãi 40% so với giá vốn thì giá tiền cửa hàng cần bán là:
\(180000\left(1+40\%\right)=180000\cdot1,4=252000\left(đồng\right)\)

\(29\cdot5^{2024}-3\cdot25^x=14\cdot5^{2024}\)
=>\(3\cdot5^{2x}=29\cdot5^{2024}-14\cdot5^{2024}=15\cdot5^{2024}=3\cdot5^{2025}\)
=>2x=2025
=>\(x=\dfrac{2025}{2}\)

a) \(\dfrac{2}{7}-\dfrac{2}{7}\times\dfrac{7}{12}\)
= \(\dfrac{2}{7}-\dfrac{1}{6}\)
= \(\dfrac{5}{42}\)
b) \(\dfrac{-11}{12}\times\dfrac{18}{25}+\dfrac{-11}{12}\times\dfrac{7}{25}+\dfrac{5}{12}\)
= \(\dfrac{-11}{12}\times\left(\dfrac{18}{25}+\dfrac{7}{25}\right)+\dfrac{5}{12}\)
= \(\dfrac{-11}{12}\times1+\dfrac{5}{12}\)
= \(\dfrac{-11}{12}+\dfrac{5}{12}\)
= \(\dfrac{-1}{2}\)
c) \(\left(x-\dfrac{1}{3}\right)\div\dfrac{1}{2}+\dfrac{3}{7}=5\dfrac{3}{7}\)
\(\left(x-\dfrac{1}{3}\right)\times2+\dfrac{3}{7}=5\dfrac{3}{7}\)
\(\left(x-\dfrac{1}{3}\right)\times2=5\dfrac{3}{7}-\dfrac{3}{7}\)
= \(\left(x-\dfrac{1}{3}\right)\times2=5\)
\(x-\dfrac{1}{3}=5\div2\)
\(x-\dfrac{1}{3}=\dfrac{5}{2}\)
\(x=\dfrac{5}{2}+\dfrac{1}{3}\)
\(x=\dfrac{17}{6}\)
Vậy \(x=\dfrac{17}{6}\)
e) \(\dfrac{-2}{3}x+\dfrac{1}{5}x=\dfrac{-14}{15}\)
\(x\left(\dfrac{-2}{3}+\dfrac{1}{5}\right)=\dfrac{-14}{15}\)
\(x\times\dfrac{-7}{15}=\dfrac{-14}{15}\)
\(x=\dfrac{-14}{15}:\dfrac{-7}{15}\)
\(x=2\)
Vậy \(x=2\)


12:
\(S=\dfrac{1}{2}+\dfrac{2}{4}+...+\dfrac{10}{2^{10}}\)
\(=\dfrac{1}{2^1}+\dfrac{2}{2^2}+...+\dfrac{10}{2^{10}}\)
\(=\dfrac{1+1}{2^{1-1}}-\dfrac{1+2}{2^1}+\dfrac{2+1}{2^{2-1}}-\dfrac{2+2}{2^2}+...+\dfrac{10+1}{2^{10-1}}-\dfrac{10+2}{2^{10}}\)
\(=2-\dfrac{12}{2^{10}}=\dfrac{2^{11}-12}{2^{10}}\)