Bài 1: Giải phương trình:
a)
b) (x+5)(x+2) – 3(4x-3) = (5 – x) 2
c) ( 3x – 1) 2 – 5( 2x + 1)2 + ( 6x – 3) ( 2x+ 1) = ( x – 1)2
Bài 2: Giải phương trình:
a)
b)
Bài 3: Giải Phương trình với tham số a, b
a) a ( ax+ b) = b2 (x – 1)
b) a2x – ab = b2( x- 1)
Bài 4: Giải phương trình mới tham số a
a)
b)
c)

Bài 1: Giải phương trình:
a)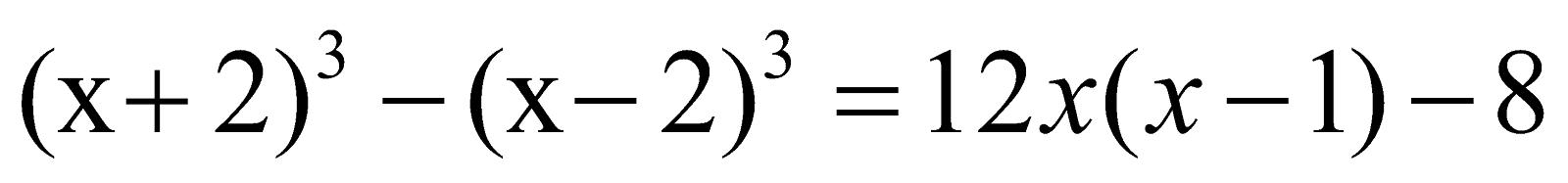
b) (x+5)(x+2) – 3(4x-3) = (5 – x) 2
c) ( 3x – 1) 2 – 5( 2x + 1)2 + ( 6x – 3) ( 2x+ 1) = ( x – 1)2
Bài 2: Giải phương trình:
a)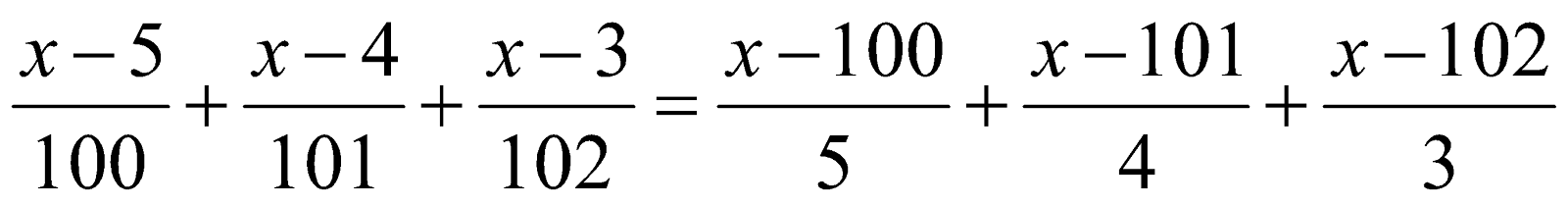
b)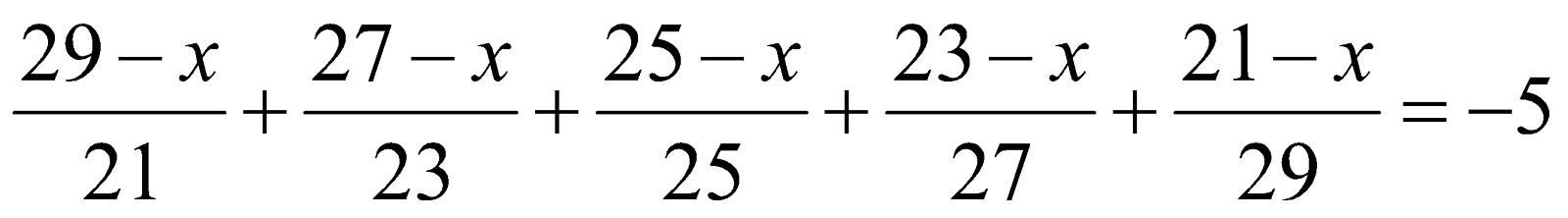
Bài 3: Giải Phương trình với tham số a, b
a) a ( ax+ b) = b2 (x – 1)
b) a2x – ab = b2( x- 1)
Bài 4: Giải phương trình mới tham số a
a)
b)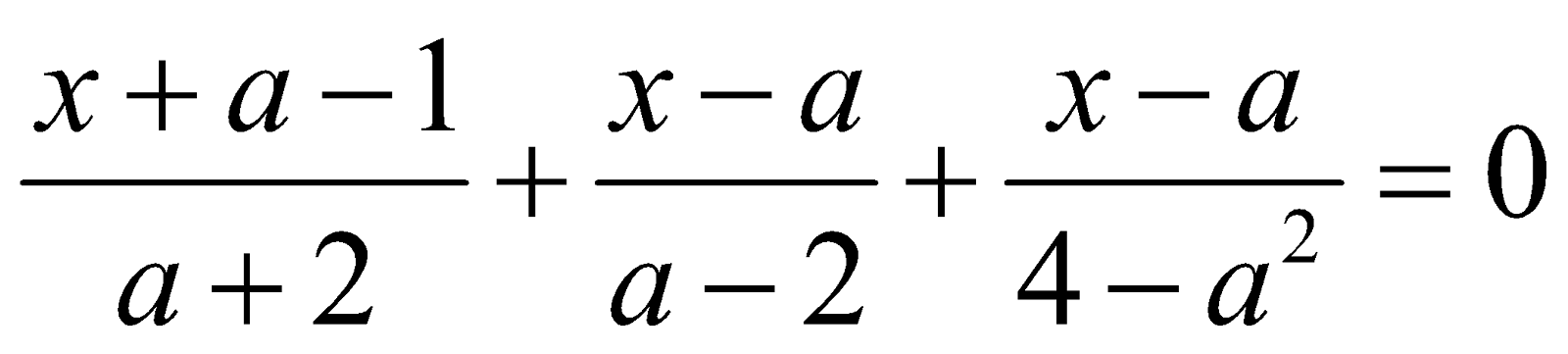
c)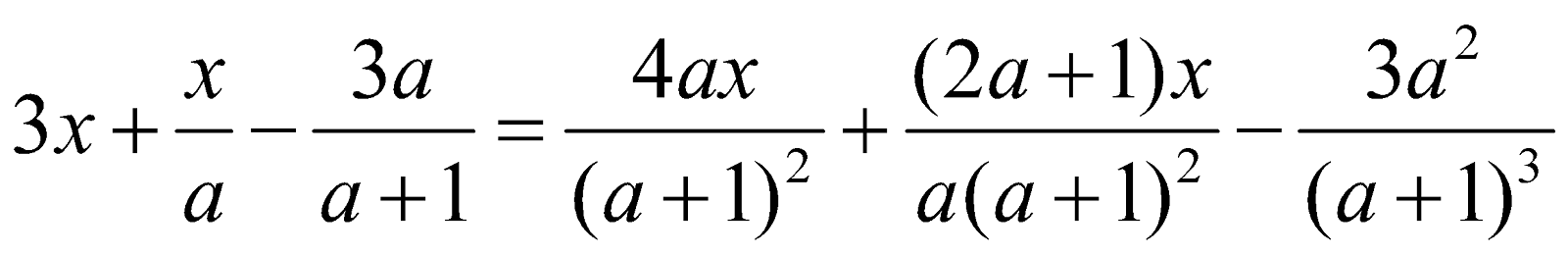
\(\left(x+5\right)\left(x+2\right)-3\left(4x-3\right)=\left(5-x\right)2\)
\(\Leftrightarrow x^2+7x+10-12x+9=10-2x\)
\(\Leftrightarrow x^2-3x+9=0\)
Mà \(x^2-3x+9>0\)nên pt vô nghiệm