Chiều dài của mảnh đất là:

\(12,5:\dfrac{5}{11}=27,5\left(m\right)\)

Diện tích của mảnh đất là:

\(12,5\times27,5=343,75\left(m^2\right)\)

ĐS: ... 

Chiều dài của miếng đất hình chữ nhật là:

     12,5 : \(\dfrac{5}{11}\) = 27,5 ( m )

Diện tích miếng đất hình chữ nhật đó là :

    12,5 x 27,5 = 343,75 ( \(m^2\) )

          Đ/S : ............

BM và BN lần lượt là các tia phân giác của các góc trong và các góc ngoài tại đỉnh B của ΔABC

=>BM và BN là hai tia phân giác của hai góc kề bù

=>\(\widehat{MBN}=90^0\)

=>ΔBMN vuông tại B

1 + 2 + 3 + ... + x

Số lượng số hạng: 

(x - 1) : 1 + 1 = x (số hạng)

Tổng của dãy số: \(\dfrac{\left(x+1\right)x}{2}\)

\(=>\dfrac{\left(x+1\right)x}{2}=190\\ =>x\left(x+1\right)=380\\ =>x^2+x-380=0\\ =>\left(x^2-19x\right)+\left(20x-380\right)\\ =>x\left(x-19\right)+20\left(x-19\right)=0\\ =>\left(x-19\right)\left(x+20\right)=0\\ TH1:x-19=0\\ =>x=19\\ =>TH2:x+20=0\\ =>x=-20\)

Mà: x > 0 => x = 19 

1 + 2 + 3 + ....... + x = 190 

Tổng trên có x số hạng 

=> ( x + 1 ) \(\times\) x : 2 = 190 

    ( x + 1 ) x  x       = 190 x 2

    ( x + 1 ) x x        = 380

   ( x + 1) x x          = 20 x 19 

Vì ( x + 1 ) và x là 2 số tự nhiên liên tiếp nên x = 19

vậy x = 19 

Gọi T là giao điểm của EF và BC. M là trung điểm DT.

Ta thấy \(AF=AE;BF=BD;CD=CE\) nên \(\dfrac{DB}{DC}.\dfrac{EC}{EA}.\dfrac{FA}{FB}=1\)

Theo định lý Menalaus, ta có \(\dfrac{TB}{TC}.\dfrac{EC}{EA}.\dfrac{FA}{FB}=1\)

\(\Rightarrow\dfrac{DB}{DC}=\dfrac{TB}{TC}\)  (1)

Đặt \(MD=MT=x;MB=b;MC=c\). Khi đó từ (1) có:

\(\dfrac{MD-MB}{MC-MD}=\dfrac{MB+MT}{MC+MT}\)

\(\Leftrightarrow\dfrac{x-b}{c-x}=\dfrac{b+x}{c+x}\)

\(\Leftrightarrow xc+x^2-bc-bx=bc-bx+cx-x^2\)

\(\Leftrightarrow x^2=bc\)

\(\Leftrightarrow MT^2=MD^2=MH^2=MB.MC\)

\(\Leftrightarrow\dfrac{MH}{MC}=\dfrac{MB}{MH}\)

Tam giác MBH và MHC có:

\(\dfrac{MH}{MC}=\dfrac{MB}{MH}\) và \(\widehat{HMB}\) chung

\(\Rightarrow\Delta MBH\sim\Delta MHC\left(c.g.c\right)\)

\(\Rightarrow\widehat{MHB}=\widehat{MCH}\)

Lại có \(\widehat{MHT}=\widehat{MTH}\) 

\(\Rightarrow\widehat{MHB}+\widehat{MHT}=\widehat{MCH}+\widehat{MTH}\)

\(\Rightarrow\widehat{BHT}=\widehat{CHE}\) (vì \(\widehat{CHE}\) là góc ngoài tại H của tam giác CHT)

\(\Rightarrow90^o-\widehat{BHT}=90^o-\widehat{CHE}\)

\(\Rightarrow\widehat{BHD}=\widehat{CHD}\)

\(\Rightarrow\) HD là tia phân giác của \(\widehat{BHC}\) (đpcm)

Số giây để in hết 1800 trang giấy là:

1800 × 5 = 9000 (giây)

Đổi 9000 giây = 150 phút = 2.5 giờ 

Số phút để máy nghỉ là:

4 × 5 = 20 (phút)

Thời gian để in hết 1800 trang giấy là:

150 + 20 = 170 (phút)

Vậy cần 170 phút để in hêt 1800 trang giấy.

NHƯ NÀY ĐÚNG KO

a: Ta có: \(\widehat{A'OC}+\widehat{AOC}=180^0\)(kề bù)

=>\(\widehat{AOC}+90^0=180^0\)

=>\(\widehat{AOC}=90^0\)

Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\widehat{AOB}< \widehat{AOC}\)

nên tia OB nằm giữa hai tia OA và OC

=>\(\widehat{AOB}+\widehat{BOC}=\widehat{AOC}\)

=>\(\widehat{BOC}=90^0-45^0=45^0\)

Ta có: \(\widehat{AOB}=\widehat{BOC}\)

mà tia OB nằm giữa hai tia OA và OC

nên OB là phân giác của góc AOC

b: Ta có: \(\widehat{COB}+\widehat{COE}=180^0\)(hai góc kề bù)

=>\(\widehat{COE}+45^0=180^0\)

=>\(\widehat{COE}=135^0\)

1) a - 2; a - 3; a - 4 

2) a + 5; a + 4; a + 3 

a - 2 ; a - 3 ; a - 4 

a + 5 ; a + 4 ; a + 3

    56 + 34 + 56 + 61 + 4 + 56 + 56 

= (56 + 56 + 56 +56) + (34 + 61 + 4)

= 56 x 4 + (95 + 4)

= 224 + 99

= 323

56 + 34 + 56 + 61 + 4 + 56 + 56

= 56 x 4 + (34 + 61 + 4)

= 224 + 99

= 224 + 100 - 1

= 324 - 1

= 323

1) 

a + 1; a; a - 1

2) 

a - 1; a - 2; a - 3 

3) 

a + b; a + b - 1; a + b - 2 

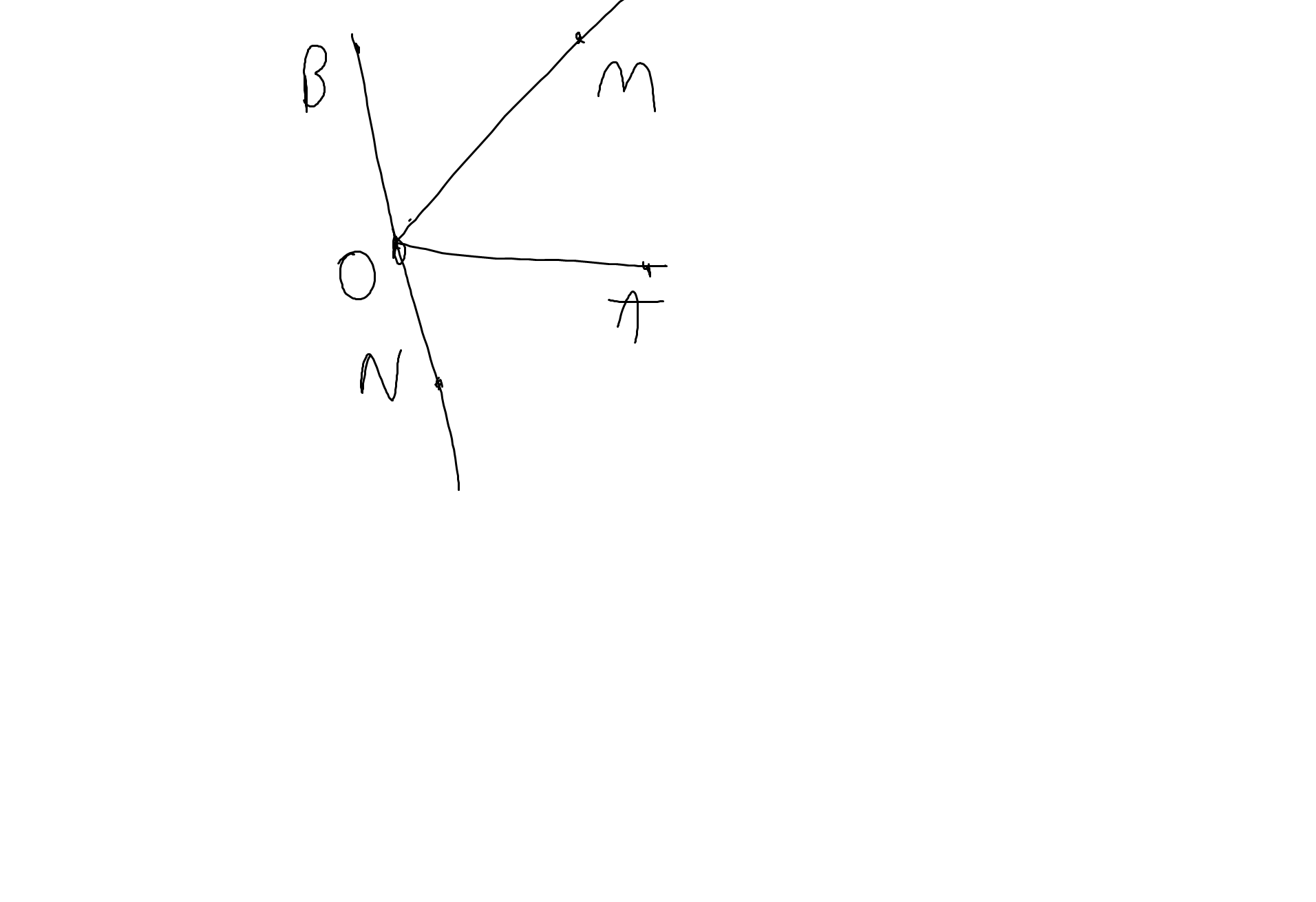
Bài 1:

a: OM là phân giác của góc AOB

=>\(\widehat{AOM}=\dfrac{\widehat{AOB}}{2}=\dfrac{120^0}{2}=60^0\)

b: Vì OM và OM là hai tia trùng nhau

nên \(\widehat{MOM}=0^0\)