Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


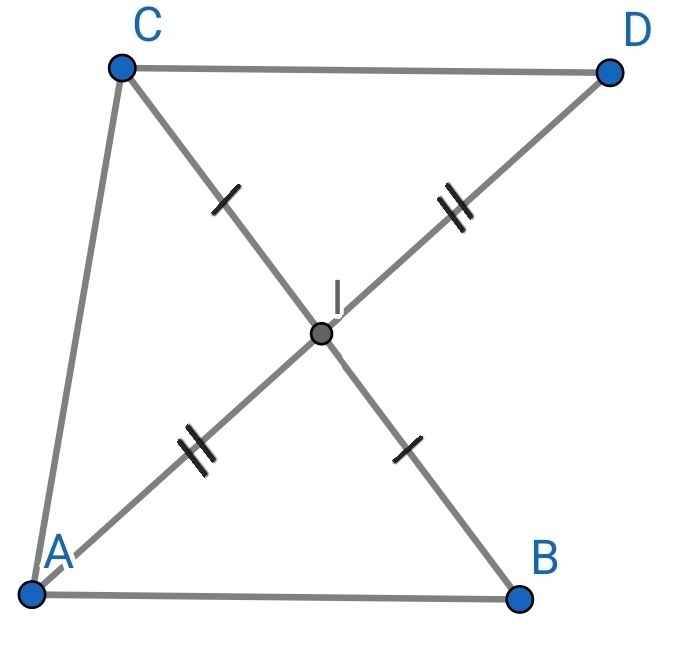 a) Xét ∆CDI và ∆BAI có:
a) Xét ∆CDI và ∆BAI có:
CI = BI (do I là trung điểm của BC)
∠CID = ∠BIA (đối đỉnh)
ID = IA (gt)
⇒ ∆CDI = ∆BAI (c-g-c)
⇒ CD = AB (hai cạnh tương ứng)
b) Do CD = AB (cmt)
Mà AB < AC (gt)
⇒ AC > CD
∆ACD có:
AC > CD (cmt)
⇒ ∠ADC > ∠CAD (quan hệ giữa góc và cạnh đối diện trong tam giác)
⇒ ∠IDC > ∠CAI
Do ∆CDI = ∆BAI (cmt)
⇒ ∠IDC = ∠BAI (hai góc tương ứng)
Mà ∠IDC > ∠CAI
⇒ ∠BAI > ∠CAI


Tk nhé bn:
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đó: ΔBAD=ΔBED
=>BA=BE
=>ΔBAE cân tại B
b: ΔBAD=ΔBED
=>góc BED=90 độ
=>DE vuông góc với BC
c: ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trực của AE

\(\dfrac{1}{R\left(x\right)}=\dfrac{1}{x\left(x+2\right)}=\dfrac{1}{2}\left(\dfrac{1}{x}-\dfrac{1}{x+2}\right)\)
\(\Rightarrow S=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2022}-\dfrac{1}{2024}+\dfrac{1}{2023}-\dfrac{1}{2025}\right)+\dfrac{1}{2.2023}\)
\(=\dfrac{1}{2}\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{2024}-\dfrac{1}{2025}\right)+\dfrac{1}{2.2023}\)
Một kết quả rất xấu

@Lê Thanh Sơn
Bạn phải giải chi tiết ra thì bạn Thu Thủy mới hiểu đc chứ đâu phải vèo cái đáp số lun đc!