Cho tam giác ABC. D là điểm chính giữa cạnh BC. E là điểm chính giữa cạnh AC. AD và BE cắt nhau ở I. So sánh diện tích 2 tam giác IAE và IBD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đây là toán nâng cao phép chia có dư, cấu trúc thi chuyên, thi học sinh giỏi các cấp, thi violympic. Hôm nay, Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải
Coi số chia là một phần thì theo bài ra ta có sơ đồ:
Theo bài ra ta có sơ đồ:
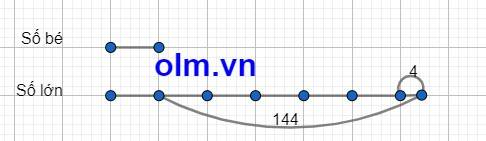
Số bé là: (144 - 4) : (6 - 1) = 28
Số lớn là: 28 x 6 + 4 = 172
Đáp số: số bé 28
số lớn 172

Số lít dầu đựng trong 1 thùng:
\(400:16=25\left(l\right)\)
Số thùng đựng được 425 lít dầu:
\(425:25=17\)(thùng)
Đáp số: 17 thùng
Trong 1 thùng có số l dầu là
400:16=25(l)
Có 425 l dầu thì cần số thùng là
425:25=17(thùng)
Đáp số:17 thùng
Chúc bn học tốt❤


Bán kính hình tròn:
\(\dfrac{6}{2}=3\left(cm\right)\)
Diện tích hình tròn:
\(3\times3\times3,14=28,26\left(cm^2\right)\)
Diện tích phần tô màu:
\(28,26\times\dfrac{60}{100}=16,956\left(cm^2\right)\)
Diện tích tam giác ABC:
\(28,26-16,956=11,304\left(cm^2\right)\)
Đáp số: 11,304 cm2

5:
a: 3,5 giờ=3h30p
6,4 giờ=6h24p
12,6 giờ=12h36p
22,2 giờ=22h12p
b: 2 giờ 15 phút=2,25 giờ
14 giờ 24 phút=14,4 giờ
9 giờ 36 phút=9,6 giờ
45 phút=0,75 giờ
Bài 3:
a: \(3m^3528dm^3=3,528m^3\)
\(8m^38dm^3=8,008m^3\)
\(12320dm^3=12,32m^3\)
\(95dm^3=0,095m^3\)
b: \(1dm^3174cm^3=1,174dm^3\)
\(2dm^378cm^3=2,078dm^3\)
\(301cm^3=0,301dm^3\)
\(9cm^3=0,009dm^3\)


Câu 5:
a: Diện tích hình vuông là \(5^2=25\left(cm^2\right)\)
Câu 4: Đặt \(A=\overline{17x8y}\)
A chia hết cho 5 nên y=0 hoặc y=5
TH1: y=0
A chia hết cho 9
=>\(1+7+x+8+0⋮9\)
=>\(x+16⋮9\)
=>x=2
TH2: y=5
A chia hết cho 9
=>\(1+7+x+8+5⋮9\)
=>\(x+21⋮9\)
=>x=6
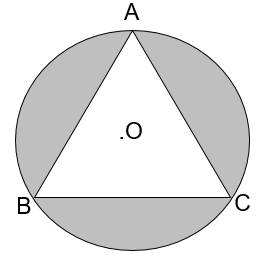


Vì E là điểm chính giữa của AC nên AE = EC = \(\dfrac{1}{2}\)AC.
Nối I với C, ta có:
\(S_{ABE}=S_{BEC}\)(Vì 2 tam giác có chung đường cao hạ từ B xuống AC, đáy AE = EC).
\(S_{IAE}=S_{IEC}\)(Vì 2 tam giác có chung đường cao hạ từ I xuống AC, đáy AE = EC)
Suy ra \(S_{IBA}=S_{IBC}\).
Vì D là điểm chính giữa của BC nên BD = DC = \(\dfrac{1}{2}\)BC.
\(S_{IBD}=\dfrac{1}{2}S_{IBC}\)(Vì 2 tam giác có chung đường cao hạ từ I xuống BC, đáy BD = \(\dfrac{1}{2}\)BC).
\(S_{ABD}=S_{ADC}\)(Vì 2 tam giác có chung đường cao hạ từ A xuống BC, đáy BD = DC).
Suy ra \(S_{ABI}=S_{BIC}=S_{AIC}\).
\(S_{IAE}=\dfrac{1}{2}S_{AIC}\)(Vì 2 tam giác có chung đường cao hạ từ I xuống AC, đáy AE = \(\dfrac{1}{2}\)AC).
Mà \(S_{BIC}=S_{AIC}\) suy ra \(S_{IAE}=\dfrac{1}{2}S_{BIC}\).
Suy ra \(S_{IAE}=S_{IBD}\).