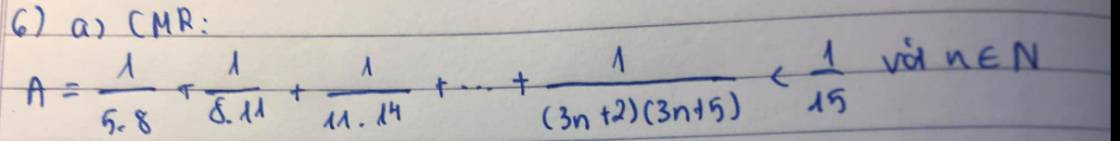
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`(x+1)^2 -|3-2x| +6 = (x+2)^2`
`<=> x^2 +2x +1 -|3-2x| +6 = x^2 +4x +4`
`<=> 2x +7 -4x -4 -|3-2x| =0`
`<=> 3 -2x -|3-2x| =0`
`<=> |3-2x| = 3-2x`
`@` nếu` 3-2x >= 0 => x <= 3/2 => |3-2x| =3-2x`
`=>` PT có dạng
`3-2x =3-2x(luôn-đúng)`
`=>` PT luôn có nghiệm khi `x<=3/2`
`@` nếu` 3-2x <0 => x >3/2 => |3-2x| = 2x-3`
`=> PT có dạng
`2x-3 = 3-2x`
`<=> 2x +2x = 3+3`
`<=> 4x=6`
`=> x = 3/2( loại)`

Gọi D là giao điểm AO và MN
Theo câu 3/ ta có \(\widehat{ABC}=\widehat{ANH}\)
Mà \(\widehat{ABC}=\widehat{CAH}\) (cùng phụ \(\widehat{ACB}\))
\(\Rightarrow\widehat{ANH}=\widehat{CAH}\)
Mà \(\widehat{CAH}+\widehat{OCA}=90^0\) (\(\Delta CAH\) vuông tại H)
\(\Rightarrow\widehat{ANH}+\widehat{OCA}=90^0\) (1)
Trong tam giác vuông ABC, AO là trung tuyến ứng với cạnh huyền
\(\Rightarrow AO=\dfrac{1}{2}BC=OC\Rightarrow\Delta OAC\) cân tại O
\(\Rightarrow\widehat{OCA}=\widehat{OAC}\) (2)
(1);(2) \(\Rightarrow\widehat{ANH}+\widehat{OAC}=90^0\)
\(\Rightarrow\widehat{ADN}=180^0-\left(\widehat{ANH}+\widehat{OAC}\right)=90^0\)
Hay \(MN\perp AO\)
Trước tiên ta cần giải quyết vế dài dòng nhất đã là vế A :
Ta có :
\(A=\dfrac{1}{5.8}+\dfrac{1}{8.11}+\dfrac{1}{11.14}+...+\dfrac{1}{\left(3n+2\right)\left(3n+5\right)}\)
\(A=\dfrac{1}{3}.\left(\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}+...+\dfrac{1}{3n+2}-\dfrac{1}{3n+5}\right)\)
Rút gọn đi ta được :
\(A=\dfrac{1}{3}.\left(\dfrac{1}{5}-\dfrac{1}{3n+5}\right)\)
\(A=\dfrac{1}{3}.\dfrac{3n+5-5}{5\left(3n+5\right)}\)
\(A=\dfrac{n}{5\left(3n+5\right)}\)
Bây giờ ta chỉ còn so sánh A với \(\dfrac{1}{5}\) là xong :
Ta có : \(\dfrac{1}{15}=\dfrac{3n+5}{15\left(3n+5\right)}\)
\(\dfrac{n}{5\left(3n+5\right)}=\dfrac{3n}{15\left(3n+5\right)}\)
Do \(n\in N\) nên : \(\dfrac{3n}{15\left(3n+5\right)}< \dfrac{3n+5}{15\left(3n+5\right)}\)
\(\Rightarrow\dfrac{n}{5\left(3n+5\right)}< \dfrac{1}{15}\)
\(\Rightarrowđpcm\)