Cho tam giác ABC vuông tại A , tia phân giác của góc ABC cắt AC tại D . Trên cạnh ABC lấy điểm E sao cho BE = BA a) Chứng minh tam giác BAD= tam gác BED b) Gọi F là giao điểm của hai đường DE và AB . Chứng minh AF=EC c) Chứng minh AE // với FC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

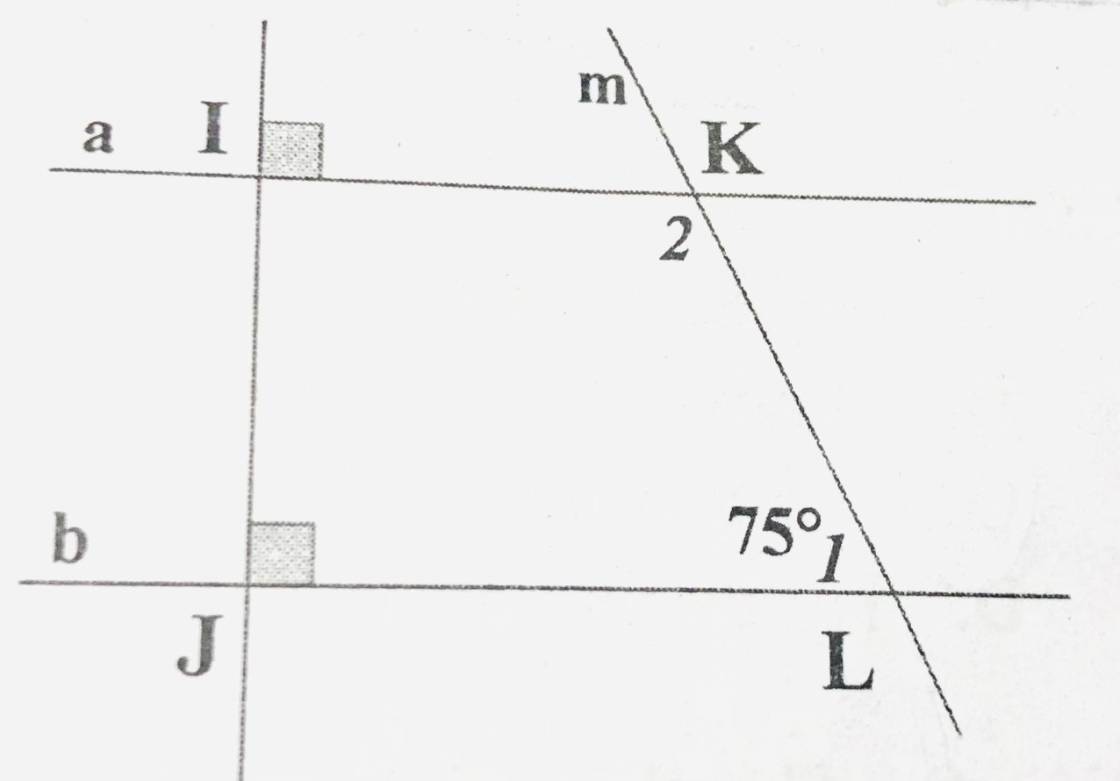
a \(\perp\) IJ
b \(\perp\) IJ
⇒ a//b (Vì trong cùng một mặt phẳng hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
\({}\)\(\widehat{K_2}\) + \(\widehat{L_1}\)= 1800 (hai góc trong cùng phía có tổng bằng 1800)
\({}\) \(\widehat{K_2}\) = 1800 - 750
\({}\) \(\widehat{K_2}\) = 1050

Các ký hiệu toán bị lỗi hết rồi bạn. Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.

Ta có: \(\left\{{}\begin{matrix}\left(x+5\right)^2\ge0\forall x\\\left|x-y+1\right|\ge0\forall x,y\end{matrix}\right.\)
\(\Rightarrow\left(x+5\right)^2+\left|x-y+1\right|\ge0\forall x,y\)
\(\Rightarrow-\left[\left(x+5\right)^2+\left|x-y+1\right|\right]\le0\forall x,y\)
\(\Rightarrow-\left(x+5\right)^2-\left|x-y+1\right|\le0\forall x,y\)
\(\Rightarrow P=-\left(x+5\right)^2-\left|x-y+1\right|+2018\le2018\forall x,y\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}x+5=0\\x-y+1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-5\\y=x+1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-5\\y=-4\end{matrix}\right.\)
Vậy \(Max_P=2018\) khi \(x=-5;y=-4\).
$Toru$


Lời giải:
Vì $I$ nằm trên đường trung trực của $BC$ nên $BI=CI$
Vì $I$ nằm trên đường phân giác $\widehat{BAC}$ nên khoảng cách từ $I$ đến $AB$ bằng khoảng cách từ $I$ đến $AC$
$\Rightarrow IH=IK$
Xét tam giác vuông $IHB$ và $IKC$ có:
$IH=IK$ (cmt)
$IB=IC$ (cmt)
$\Rightarrow \triangle IHB=\triangle IKC$ (ch-gn)
$\Rightarrow HB=KC$ (đpcm)
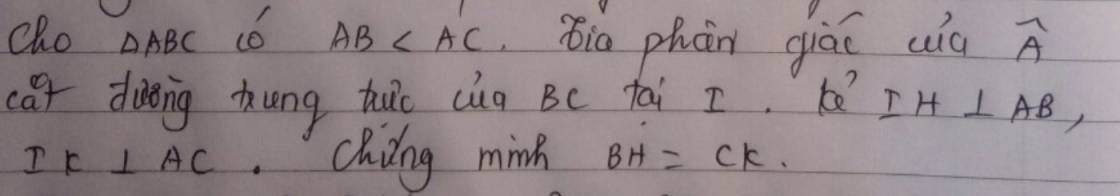 vẽ hình cho mik luôn nhé
vẽ hình cho mik luôn nhé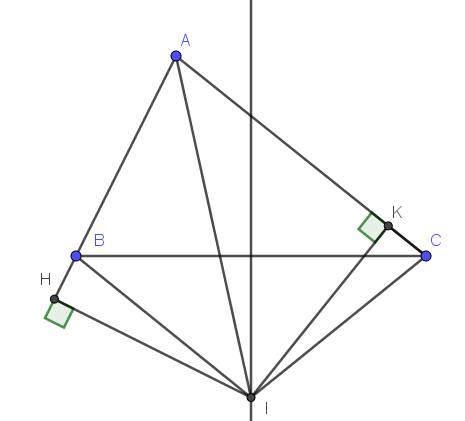
a) C/m tam giác BAD = tam giác BED
xét tam giác BAD và tam giác BED, ta có
BD chung
BA = BE (gt)
ABD = DBE (BD tia phân giác góc ABC)
=>tam giác BAD = tam giác BED
=>AD=DE( cặp cạnh tương ứng)
b) chứng minh AF = EC
Xét tam giác ADF và tam giác EDC, ta có
AD = DE( cmt )
ADF = EDC( đối đỉnh )
DAF=DEC( = 900)
=>tam giác ADF = tam giác EDC
=>AF = EC ( cặp cạnh tương ứng)
=>ECA=AFE(cặp góc tương ứng )
c) C/M AE // FC
tam giác BEC có
BE = BA ( gt )
=> tam giác BEC cân cại B
=>BEA=BAE
ta có
ED = AD
DF = DC
=>ED+DF=AD+DC
=>EF=AC
xét tam giác ACF và tam giác EFC, ta có
EC = AF (cmt)
CF chung
EF=AC(cmt)
=>tam giác ACF= tam giác EFC
=>EFC=ACF(cặp góc tương ứng)
ta có:
ECA = AFE(cmt)
ACF=EFC(cmt)
=>ECA+ACF=AFE+EFC
=>ECF=AFC
tam giác BCF có
BCF=BFC(cmt)
=>tam giác BCF cân tại B
Ta có
tam giác BEC cân tại B
tam giác BCF cân tại B
=>BEA=BCF=BAE=BFC
mà BEA đồng vị BCF
=> AE//FC
cái câu c mình ko chắc đúng lắm nha.('v')