Tìm các số nguyên x,y biết:(x+3)(1-x)=|y|
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Xét tam giác AEB và tam giác DEC có: BE=EC( E là trđ của BC. AE= DE( gt) góc AEB= góc DEC(2 góc đối đỉnh) suy ra tâm giác AEB= tam giác DEC. b. Xét ABDC có: AE=ED. BE= CE. suy ra ABDC là hbh (dhnb)


\(\dfrac{1}{3}\) - |\(\dfrac{3}{4}\) - \(x\)| = 12
|\(\dfrac{3}{4}\) - \(x\)| = \(\dfrac{1}{3}\) - 12
| \(\dfrac{3}{4}\) - \(x\)| = - \(\dfrac{35}{3}\)
Vì |\(\dfrac{3}{4}\) - \(x\)| ≥ 0 ⇒ - \(\dfrac{35}{3}\) ≥ 0 (vô lý)
Vậy không có giá trị nào của \(x\) thỏa mãn đề bài

câu 5: đáp án là C nhé bạn
Câu 6: Căn bậc hai số học của 25 là: 5 -5 cộng trừ 5 225

a, \(\dfrac{15}{4}\) - 2,5 : |\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3
3,75 - 2,5:|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3
2,5:|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3,75 - 3
2,5 : |\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 0,75
|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 2,5 : 0,75
|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = \(\dfrac{10}{3}\)
\(\left[{}\begin{matrix}\dfrac{3}{4}x+\dfrac{1}{2}=-\dfrac{10}{3}\\\dfrac{3}{4}x+\dfrac{1}{2}=\dfrac{10}{3}\end{matrix}\right.\)
\(\left[{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{10}{3}-\dfrac{1}{2}\\\dfrac{3}{4}x=\dfrac{10}{3}-\dfrac{1}{2}\end{matrix}\right.\)
\(\left[{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{26}{3}\\\dfrac{3}{4}x=\dfrac{17}{6}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-\dfrac{46}{9}\\x=\dfrac{34}{9}\end{matrix}\right.\)




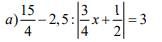 Cíu mình với=(((
Cíu mình với=(((
Lời giải:
Vì $|y|\geq 0$ với mọi $y$ nên:
$(x+3)(1-x)=|y|\geq 0$. Khi đó sẽ có 2 TH xảy ra:
TH1: $x+3\geq 0; 1-x\geq 0$
$\Rightarrow 1\geq x\geq -3$
Mà $x$ nguyên nên $x\in \left\{1; 0; -1; -2; -3\right\}$
Nếu $x=1$ thì: $|y|=0\Rightarrow y=0$
Nếu $x=0$ thì $|y|=3\Rightarrow y=\pm 3$
Nếu $x=-1$ thì $|y|=4\Rightarrow y=\pm 4$
Nếu $x=-2$ thì $|y|=3\Rightarrow y=\pm 3$
Nếu $x=-3$ thì $|y|=0\Rightarrow y=0$
TH2: $x+3\leq 0; 1-x\leq 0\Rightarrow x\geq 1$ và $x\leq -3$ (vô lý) - loại.