Cho $a, b, c$ là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức $P=\dfrac{3(b+c)}{2 a}+\dfrac{4 a+3 c}{3 b}+\dfrac{12(b-c)}{2 a+3 c}$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi \(x\) (nghìn đồng) là giá niêm yết của quạt điện \(\left(0< x< 900\right)\)
Vì tổng số tiền theo giá niêm yết của 2 sản phẩm là 900 nghìn đồng nên giá niêm yết của đèn tích điện là \(900-x\) (nghìn đồng)
Vì thực tế giá quạt điện giảm \(15\%\) nên giá quạt lúc này là \(x-15\%x=85\%x=\dfrac{17}{20}x\)
Vì thực tế giá bóng đèn tích điện giảm \(10\%\) nên giá quạt lúc này là \(\left(900-x\right)-10\%\left(900-x\right)=900-x-90+10\%x\)\(810-90\%x=810-\dfrac{9}{10}x\)
Do tổng số tiền thực tế người đó phải trả 780 nghìn đồng nên ta có phương trình \(\dfrac{17}{20}x+\left(810-\dfrac{9}{10}x\right)=780\Leftrightarrow\dfrac{1}{20}x=30\Leftrightarrow x=600\) (nhận)
Vậy giá niêm yết của quạt điện là 600 nghìn đồng còn đèn tích điện là 300 nghìn đồng.

x2-4x-5=0
⇔x2-5x+x-5=0
⇔(x2+x)-(5x+5)=0
⇔x(x+1)-5(x+1)=0
⇔(x-5)(x+1)=0
⇔\(\left\{{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
vậy phương trình có 2 nghiệm phân biệt x=5;x=-1
b, A=\(\dfrac{x}{x-4}\)+\(\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\)
=\(\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{2\sqrt{x}+x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{\sqrt{x}\left(2+\sqrt{x}\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)}\)

28=2.2.7
12 = 2.2.3
em nhân \(\sqrt{7}\)vào ngoặc thì ra ... chỉ còn 7 thôi

bài này không thể dùng cosi được nên là:
do x2 ≥ 0
⇔ x2+3≥3
⇔1/(x2+3)≥1/3
⇔x2+1/(x2+3)≥1/3 (do x2≥0)
=>GTNN A=1/3 khi x=0

Đúng như bạn Quang viết, GTNN của S là 13 khi \(\left\{{}\begin{matrix}a=2\\b=3\\c=4\end{matrix}\right.\), nhưng mình cần một lời giải thích vì sao nó lại ra như vậy.

Vì (d1)//(d2) nên 4m=4 ⇔ m=1
Khi đó ta có pt (d1): y=4x+n
Vì (d2) đi qua điểm A(2;0) nên ta có:
0=4\(\times\)2+n ⇔ 8+n=0 ⇔ n=\(_{^{ }-8}\)
Vậy m=1 và n= -8
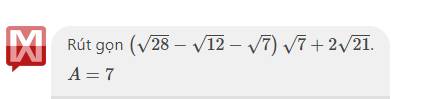 tại sao rú gọn lại ra kết quả nnay ạ gthich giúp e
tại sao rú gọn lại ra kết quả nnay ạ gthich giúp e