thu gọn biểu thức C+D biết: C=5^3+5^5+...+5^101 và D=1+3^2+3^4+3^6+...+3^100 lớp 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta thấy: \(\left|x-y-5\right|\ge0\forall x;y\)
\(\left(y-3\right)^4\ge0\forall y\)
\(\Rightarrow\left|x-y-5\right|+\left(y-3\right)^4\ge0\forall x;y\)
Mặt khác: \(\left|x-y-5\right|+\left(y-3\right)^4=0\)
nên: \(\left\{{}\begin{matrix}x-y-5=0\\y-3=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=y+5\\y=3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=8\\y=3\end{matrix}\right.\)
Vậy \(x=8;y=3\).

Bài 11:
Gọi số học sinh giỏi 4 khối lần lượt là $a,b,c,d$ (em)
Theo bài ra ta có: $a+b+c-d=168$ và $\frac{a}{13}=\frac{b}{12}=\frac{c}{14}=\frac{d}{15}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{13}=\frac{b}{12}=\frac{c}{14}=\frac{d}{15}=\frac{a+b+c-d}{13+12+14-15}=\frac{168}{24}=7$
$\Rightarrow a=13.7=91; b=12.7=84; c=14.7=98; d=15.7=105$
Bài 12:
Gọi số học sinh ba khối lần lượt là $a,b,c$ (học sinh).
Theo bài ra ta có: $\frac{a}{10}=\frac{b}{9}=\frac{c}{8}$ và $a-b=50$
Áp dụng TCDTSBN:
$\frac{a}{10}=\frac{b}{9}=\frac{c}{8}=\frac{a-b}{10-9}=\frac{50}{1}=50$
$\Rightarrow a=50.10=500; b=50.9=450; c=50.8=400$ (hs)

Bài 11
Gọi x (học sinh), y (học sinh), z (học sinh), t (học sinh) lần lượt là số học sinh giỏi của khối 6; 7; 8; 9 (x, y, z, t ∈ ℕ*)
Do số học sinh giỏi của khối 6; 7; 8; 9 tỉ lệ với 13; 12; 14; 15 nên ta có:
x/13 = y/12 = z/14 = t/15
Do tổng số hocj sinh giỏi của khối 6; 7 và 8 hơn số học sinh giỏi của khối 9 là 168 em nên:
x + y + z - t = 168
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/13 = y/12 = z/14 = t/15 = (x + y + z - t)/(13 + 12 + 14 - 15) = 168/24 = 7
x/13 = 7 ⇒ x = 7.13 = 91
y/12 = 7 ⇒ y = 7.12 = 84
z/14 = 7 ⇒ z = 7.14 = 98
t/15 = 7 ⇒ t = 7.15 = 105
Vậy số học sinh giỏi của khối 6; 7; 8; 9 lần lượt là: 91 học sinh, 84 học sinh, 98 học sinh, 105 học sinh
Bài 12
Gọi x (học sinh), y (học sinh), z (học sinh) lần lượt là số học sinh cú khối 7; 8 và 9 (x, y, z ∈ ℕ*)
Do số học sinh của khối 6, khối 7, khối 8 lần lượt tỉ lệ với 10; 9; 8 nên ta có:
x/10 = y/9 = z/8
Do số học sinh khối 8 ít hơn số học sinh khối 7 là 50 em nên:
x - y = 50
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/10 = y/9 = z/8 = (x - y)/(10 - 9) = 50/1 = 50
x/10 = 50 ⇒ x = 50.10 = 500
y/9 = 50 ⇒ y = 50.9 = 450
z/8 = 50 ⇒ z = 50.8 = 400
Vậy số học sinh của khối 7, khối 8, khối 9 lần lượt là: 500 học sinh, 450 học sinh, 400 học sinh

C= 53+55+... +5101
⇔25C= 55+ 57+...+5103
⇔25C-C=(55+57+...+5103) - ( 53+55+...+5101)
⇔24C=5103 - 53
⇔C=(5103 - 53 ) / 24
CMTT : D=1 + 32+34+36+ ... + 3100
⇔9D= 32+34+36+38+...+ 3102
⇔9D-D=(32+34+36+38+...+ 3102) - (1 + 32+34+36+ ... + 3100)
⇔8D=3102-1
⇔D=(3102-1)/8
Để thu gọn biểu thức \( C D \), chúng ta cần tính giá trị của \( C \) và \( D \) trước.
Đầu tiên, ta tính giá trị của \( C \):
\[ C = 5^{3} + 5^{5} + \ldots + 5^{101} \]
Đây là một dãy số hình học với công bội là 5. Ta có thể sử dụng công thức tổng của dãy số hình học để tính tổng này. Công thức tổng của dãy số hình học là:
\[ S = \frac{a(1 - r^n)}{1 - r} \]
Trong đó:
- \( S \) là tổng của dãy số hình học
- \( a \) là số hạng đầu tiên của dãy
- \( r \) là công bội của dãy
- \( n \) là số lượng số hạng trong dãy
Áp dụng công thức này vào biểu thức \( C \), ta có:
\[ C = \frac{5^3(1 - 5^{99})}{1 - 5} \]
Tiếp theo, ta tính giá trị của \( D \):
\[ D = 1 + 3^2 + 3^4 + \ldots + 3^{100} \]
Đây là một dãy số hình học với công bội là 9. Ta cũng có thể sử dụng công thức tổng của dãy số hình học để tính tổng này. Áp dụng công thức này vào biểu thức \( D \), ta có:
\[ D = \frac{1(1 - 3^{100})}{1 - 3^2} \]
Cuối cùng, để thu gọn biểu thức \( C D \), ta tính giá trị của \( C D \) bằng cách nhân giá trị của \( C \) và \( D \):
\[ C D = \frac{5^3(1 - 5^{99})}{1 - 5} \times \frac{1(1 - 3^{100})}{1 - 3^2} \]
Bạn có thể tính giá trị cuối cùng của biểu thức \( C D \) bằng cách thực hiện các phép tính trên.

C = 53 + 55 + ... + 5101
52.C = 55 + 57 + ... + 5103
25.C - C = (55 + 57 + ... + 5103) - (53 + 55 + ... + 5101)
24C = 55 + 57 + ... + 5103 - 53 - 55 - ... - 5101
24C = (55 - 55) + (57 - 57) +...+ (5101 - 5101) + 5103 - 53
24C = 5103 - 53
C = \(\dfrac{5^{103}-5^3}{24}\)

Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk, c=dk$. Khi đó:
$\frac{a}{b}=\frac{bk}{b}=k(1)$
$\frac{a^2+c^2}{b^2+c^2}=\frac{(bk)^2+(dk)^2}{b^2+(dk)^2}=\frac{k^2(b^2+d^2)}{b^2+d^2k^2}(2)$
Từ $(1); (2)$ suy ra đề sai.

Đặt: \(\dfrac{x}{4}=\dfrac{y}{7}=k\)
\(\Rightarrow\left\{{}\begin{matrix}x=4k\\y=7k\end{matrix}\right.\)
Ta có: \(xy=112\Rightarrow4k\cdot7k=112\)
\(\Rightarrow28k^2=112\)
\(\Rightarrow k^2=4\)
\(\Rightarrow\left[{}\begin{matrix}k=-2\\k=2\end{matrix}\right.\)
Với k = -2
\(\Rightarrow\left\{{}\begin{matrix}x=4\cdot-2=-8\\y=7\cdot-2=-14\end{matrix}\right.\)
Với k = 2
\(\Rightarrow\left\{{}\begin{matrix}x=4\cdot2=8\\y=7\cdot2=14\end{matrix}\right.\)

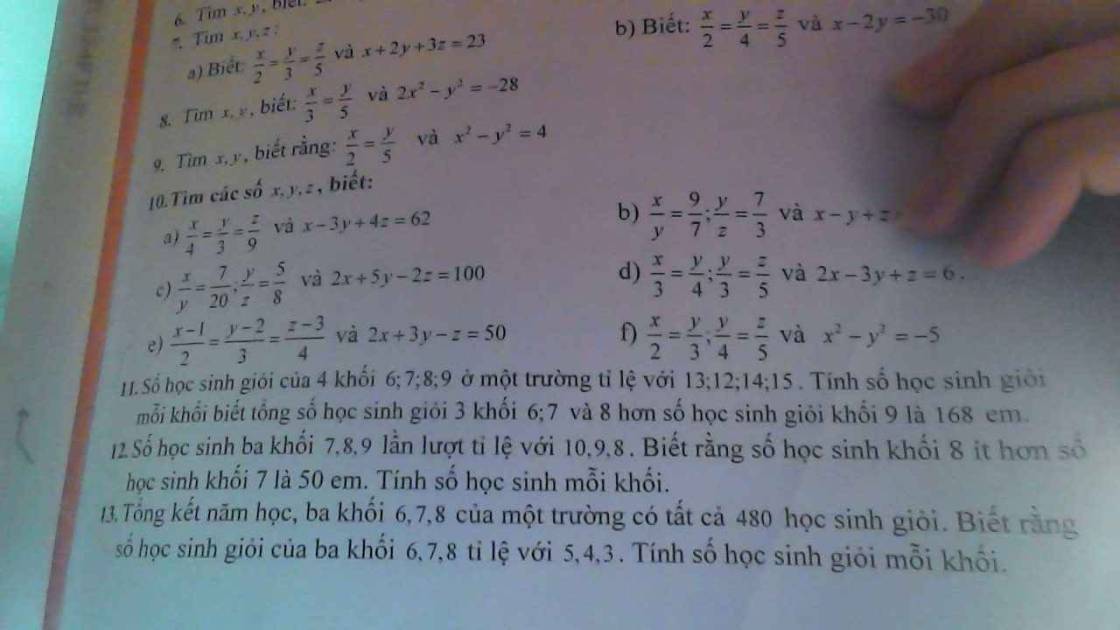
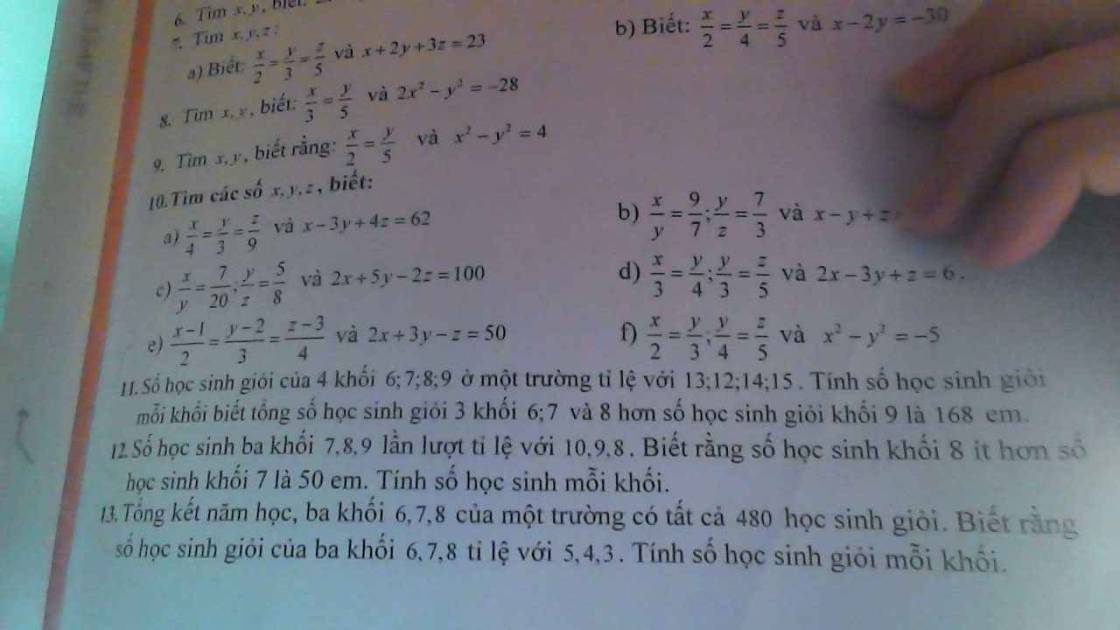
C = 5³ + 5⁵ + ... + 5¹⁰¹
⇒ 25C = 5⁵ + 5⁷ + ... + 5¹⁰¹
⇒ 24C = 25C - C
= (5⁵ + 5⁷ + ... + 5¹⁰³) - (5³ + 5⁵ + ... + 5¹⁰¹)
= 5¹⁰³ - 5⁵
⇒ C = (5¹⁰³ - 5⁵)/24
--------
D = 1 + 3² + 3⁴ + ... + 3¹⁰⁰
⇒ 9D = 3² + 3⁴ + 3⁶ + ... + 3¹⁰²
⇒ 8D = 9D - D
= (3² + 3⁴ + 3⁶ + ... + 3¹⁰²) - (1 + 3² + 3⁴ + ... + 3¹⁰⁰)
= 3¹⁰² - 1
⇒ D = (3¹⁰² - 1)/8