1.

Áp dụng tính chất dãy tỉ số bằng nhau:

$\frac{x}{5}=\frac{y}{7}=\frac{z}{10}=\frac{2x}{10}=\frac{y}{7}=\frac{z}{10}$

$=\frac{2x+y-z}{10+7-10}=\frac{-21}{7}=-3$

$\Rightarrow x=-3.5=-15; y=-3.7=-21; z=-3.10=-30$

2.

Áp dụng tính chất dãy tỉ số bằng nhau:

$\frac{x}{3}=\frac{y}{4}=\frac{z}{6}=\frac{2x}{6}=\frac{4y}{16}=\frac{3z}{18}$

$=\frac{4y-2x+3z}{16-6+18}=\frac{-56}{28}=-2$

$\Rightarrow x=-2.3=-6; y=-2.4=-8; z=-2.6=-12$

Đề rõ hơn đi ạ?

Lời giải:

Ta thấy: $\sqrt{(x-2024)^2}\geq 0$ với mọi $x\in\mathbb{R}$

$|x+y-4z|\geq 0$ với mọi $x,y,z\in\mathbb{R}$

$\sqrt{5y^2}\geq 0$ với mọi $y\in\mathbb{R}$

Do đó để tổng của chúng bằng $0$ thì bản thân mỗi số đó phải nhận giá trị $0$

Hay:
$\sqrt{(x-2024)^2}=|x+y-4z|=\sqrt{5y^2}=0$

$\Leftrightarrow x=2024; y=0; z=\frac{x+y}{4}=506$

Vì các p/s bé hơn 1 nên tổng nó bé hơn 1

thế thui

CM: A = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{4^2}\)+...+ \(\dfrac{1}{50^2}\) < 1

      \(\dfrac{1}{2^2}\)  < \(\dfrac{1}{1.2}\) = \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\)

      \(\dfrac{1}{3^2}\) < \(\dfrac{1}{2.3}\) = \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\)

      .............................

      \(\dfrac{1}{50^2}\) < \(\dfrac{1}{49.50}\) = \(\dfrac{1}{49}\) - \(\dfrac{1}{50}\)

       Cộng vế với vế ta có:

       A  < \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + ... + \(\dfrac{1}{49}\) - \(\dfrac{1}{50}\)

       A < 1 - \(\dfrac{1}{50}\)

       A < 1 (đpcm)

Lời giải:
Thể tích bể:

$50\times 25\times 2,3=2875$ (m³)

Thể tích phần không chứa nước:

$50\times 25\times 0,3=375$ (m³)

Thể tích nước trong bể:

$2875-375=2500$ (m³)

\(\left(\dfrac{2}{7}\right)^{10}\times7^{10}\\ =\dfrac{2^{10}}{7^{10}}\times7^{10}\\ =2^{10}=1024\)

Mình đg rất cần gấp giúp mình nhé 

a) Ta có:

∠BAC + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)

⇒ ∠BAC = 180⁰ - ∠B - ∠C

= 180⁰ - 73⁰ - 45⁰ = 62⁰

⇒ ∠A₁ = ∠A₂ = 62⁰ : 2

= 21⁰

⇒ x = 180⁰ - ∠B - ∠A₁

= 180⁰ - 73⁰ - 31⁰

= 76⁰

y = 180⁰ - ∠C - ∠A₂

= 180⁰ - 45⁰ - 31⁰

= 104⁰

b)

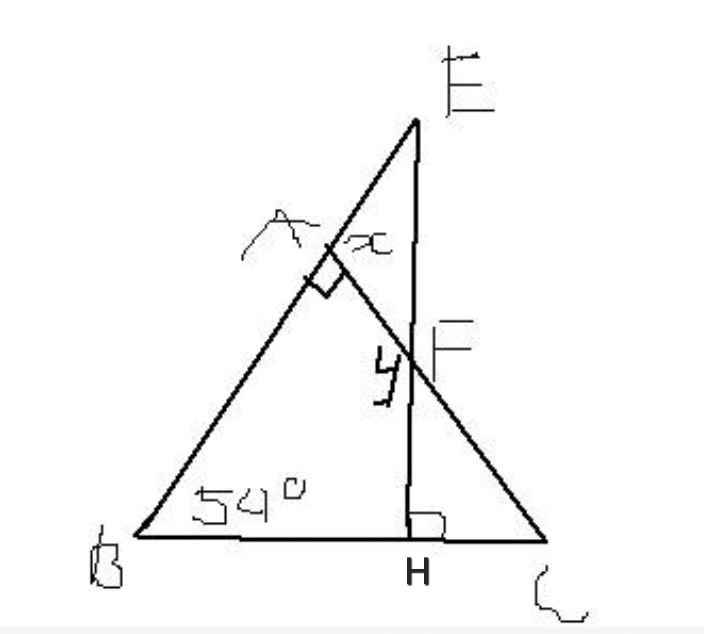
Ta có:

∠BAC + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)

⇒ ∠C = 180⁰ - ∠BAC - ∠B

= 180⁰ - 54⁰ - 90⁰

= 36⁰

Ta có:

∠C + ∠CFH + ∠CHF = 180⁰ (tổng ba góc trong ∆CHF)

⇒ ∠CFH = 180⁰ - ∠C - ∠CHF

= 180⁰ - 36⁰ - 90⁰

= 54⁰

Ta có:

y + ∠CFH = 180⁰ (kề bù)

⇒ y = 180⁰ - 54⁰

= 126⁰

x là góc nào em?

\(\dfrac{5}{18}+\dfrac{7}{15}-\dfrac{7}{21}+\left(\dfrac{-10}{36}\right)+\dfrac{8}{15}+\dfrac{1}{3}-\dfrac{4}{9}\\ =\left(\dfrac{5}{18}+\dfrac{-10}{36}\right)+\left(\dfrac{7}{15}+\dfrac{8}{15}\right)+\left(\dfrac{-7}{21}+\dfrac{1}{3}\right)-\dfrac{4}{9} \\ =0+1+0-\dfrac{4}{9}=\dfrac{5}{9}\)

tinh hop li nhe