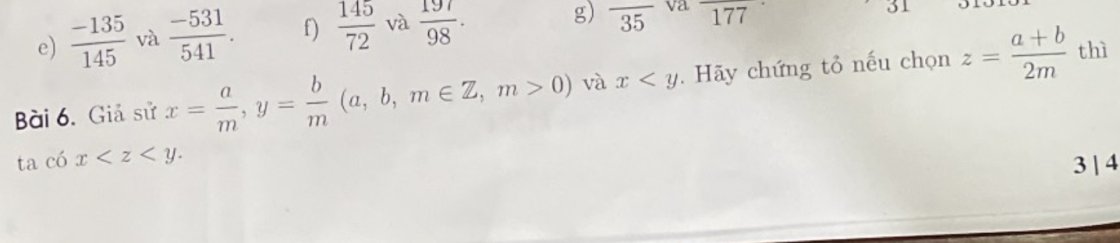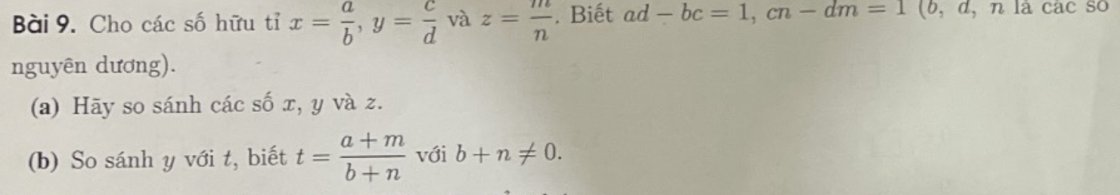b1: \(\dfrac{1}{-3}=\dfrac{-1}{3}=\dfrac{-10}{30}\)

\(\dfrac{-1}{4}=\dfrac{-10}{40}\)

=>3 số hữu tỉ xen giữa là \(-\dfrac{10}{31};-\dfrac{10}{33};-\dfrac{10}{37}\)

b2: \(\dfrac{-3}{7}=\dfrac{-3\cdot5}{7\cdot5}=\dfrac{-15}{35}=\dfrac{-150}{350};\dfrac{-2}{5}=\dfrac{-2\cdot7}{5\cdot7}=\dfrac{-14}{35}=-\dfrac{140}{350}\)

=>3 số hữu tỉ xen giữa là \(-\dfrac{149}{350};-\dfrac{147}{350};-\dfrac{145}{350}\)

a) Ta có MH//AC \(\left(\perp AB\right)\) nên \(\Delta BMH\sim\Delta BAC\)

\(\Rightarrow\dfrac{BM}{BA}=\dfrac{MH}{AC}\) \(\Rightarrow BM.AC=BA.MH\)

Tam giác ABH vuông tại H có đường cao HM 

\(BA.MH=HB.HA\)     

Tương tự, ta có: \(CN.AB=HC.HA\)

Cộng theo vế 2 hệ thức trên, ta được:

\(BA.MH+CN.AB=HB.HA+HC.HA=HA\left(HB+HC\right)=AH.BC\)

Ta có đpcm.

b) Tam giác ABH vuông tại H có đường cao HM nên \(AM.BM=MH^2\).

 Tương tự, ta có \(AN.CN=HN^2\)

 Do đó \(VT=AM.BM+AN.CN=MH^2+HN^2\)

 Dễ thấy tứ giác AMHN là hình chữ nhật nên \(MH^2+HN^2=MN^2=AH^2\)

 Tam giác ABC vuông tại A có đường cao AH nên \(AH^2=BH.CH\)

 Từ đó suy ra \(VT=BH.CH=VP\)

 Vậy đẳng thức được chứng minh.

 c) Xét hệ trục tọa độ Axy với A là gốc tọa độ, \(Ax\equiv AC,Ay\equiv AB\)

 Khi đó đặt \(B\left(0;b\right)\), \(C\left(c;0\right)\)

 Khi đó phương trình đường thẳng \(BC:y=-\dfrac{b}{c}x+b\)

 \(\Rightarrow\) Phương trình đường thẳng \(AH:y=\dfrac{c}{b}x\)

 Khi đó hoành độ của điểm H chính là nghiệm của pt hoành độ giao điểm của AH và BC: \(\dfrac{c}{b}x_0=-\dfrac{b}{c}x_0+b\)

 \(\Leftrightarrow\left(\dfrac{c}{b}+\dfrac{b}{c}\right)x_0=b\) 

 \(\Leftrightarrow\left(\dfrac{c^2+b^2}{bc}\right)x_0=b\) 

 \(\Leftrightarrow x_0=\dfrac{cb^2}{b^2+c^2}\) 

 \(\Rightarrow y_0=\dfrac{c}{b}x_0=\dfrac{c}{b}.\dfrac{cb^2}{b^2+c^2}=\dfrac{bc^2}{b^2+c^2}\)

 Vậy \(H\left(\dfrac{cb^2}{b^2+c^2},\dfrac{bc^2}{b^2+c^2}\right)\)

 Vì M là hình chiếu của H lên trục Oy \(\Rightarrow M\left(0,\dfrac{bc^2}{b^2+c^2}\right)\)

 Tương tự \(\Rightarrow N\left(\dfrac{cb^2}{b^2+c^2},0\right)\)

 Khi đó \(BM=BA-MA=b-\dfrac{bc^2}{b^2+c^2}=\dfrac{b^3+bc^2-bc^2}{b^2+c^2}=\dfrac{b^3}{b^2+c^2}\)

\(CN=CA-NA=c-\dfrac{cb^2}{b^2+c^2}=\dfrac{cb^2+c^3-cb^2}{b^2+c^2}=\dfrac{c^3}{b^2+c^2}\)

 \(\Rightarrow\dfrac{BM}{CN}=\dfrac{\dfrac{b^3}{b^2+c^2}}{\dfrac{c^3}{b^2+c^2}}=\dfrac{b^3}{c^3}=\left(\dfrac{b}{c}\right)^3=\left(\dfrac{AB}{AC}\right)^3\)

 \(\Rightarrow\sqrt[3]{\dfrac{MB}{NC}}=\dfrac{AB}{AC}\) (đpcm)

Ta có: \(x+y=\dfrac{a}{m}+\dfrac{b}{m}=\dfrac{a+b}{m}\)

\(\Rightarrow\dfrac{1}{2}\left(x+y\right)=\dfrac{1}{2}\cdot\dfrac{a+b}{m}=\dfrac{a+b}{2m}\)

\(\Rightarrow\dfrac{1}{2}\left(x+y\right)=z\)

\(\Rightarrow\dfrac{x+y}{2}=z\)

=> `z` là trung bình cộng của `x` và `y` 

=> `z` nằm giữa `x` và `y`

Mà:  `x<y`

=> `x<z<y`

Bạn cần trả lời nhiều câu hỏi và tham gia các hoạt động tích cực trên OLM là hack được rồi.

là sao

sai rồi Minh Vương
phải là
a) Lớn nhất : 9 107 531
b, bé nhất 1 075 319

lớn nhất: 9 107 531

nhỏ nhất:1 075 319

Gọi đường thẳng (d): y=ax+b(\(a\ne0\)) là đường thẳng đi qua hai điểm A(2;0) và B(-1;-5)

Thay x=2 và y=0 vào y=ax+b, ta được:

\(a\cdot2+b=0\)

=>b=0

=>y=ax

Thay x=-1 và y=-5 vào y=ax, ta được:

\(a\cdot\left(-1\right)=-5\)

=>a=5

=>y=5x

=>Phương trình cần tìm là 5x-y=0

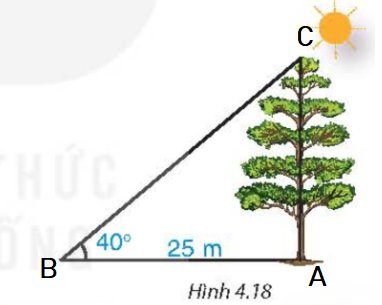
4.8:

a: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AB=\sqrt{21^2-18^2}=3\sqrt{13}\)

Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{18}{21}=\dfrac{6}{7}\)

nên \(\widehat{B}\simeq59^0\)

=>\(\widehat{C}=90^0-\widehat{B}\simeq31^0\)

b: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ABC}+30^0=90^0\)

=>\(\widehat{ABC}=60^0\)

Xét ΔABC vuông tại A có \(cosC=\dfrac{AC}{BC}=\dfrac{b}{BC}\)

=>\(\dfrac{10}{BC}=cos30=\dfrac{\sqrt{3}}{2}\)

=>\(BC=\dfrac{20\sqrt{3}}{3}\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AB=\sqrt{\left(\dfrac{20\sqrt{3}}{3}\right)^2-10^2}=\dfrac{10\sqrt{3}}{3}\)

c: ΔABC vuông tại A

=>\(BC^2=AB^2+AC^2\)

=>\(BC=5^2+3^2=\sqrt{34}\)

Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}=\dfrac{b}{c}=\dfrac{3}{5}\)

nên \(\widehat{B}\simeq30^058'\)

=>\(\widehat{C}=90^0-30^058'=59^02'\)

Bài toán được mô tả như hình sau:

Xét \(\Delta ABC\) vuông tại A có: 

\(\tan B=\dfrac{AC}{AB}\)

\(\Rightarrow AC=AB.\tan B=25.\tan40^{\circ}\approx21\left(m\right)=210\left(dm\right)\)

(x - 5) x 2 = 16

x - 5 = 16 : 2

x - 5 = 8

x = 8 + 5

x = 13

Vậy: ... 

\(\left(x-5\right)\times2=16\)

\(x-5=16:2\)

\(x-5=8\)

\(x=8+5\)

\(x=13\)

Vậy \(x=13\)