Tổng số lít xăng là:

\(105:\left(\dfrac{3}{5}-\dfrac{1}{4}\right)=105:\dfrac{7}{20}=105\times\dfrac{20}{7}=300\left(lít\right)\)

Ta có: \(\widehat{BOC}=\widehat{AOD}\)(hai góc đối đỉnh)

mà \(\widehat{BOC}=45^0\)

nên \(\widehat{AOD}=45^0\)

Ta có: \(\widehat{AOD}+\widehat{DOB}=180^0\)(hai góc  kề bù)

=>\(\widehat{DOB}+45^0=180^0\)

=>\(\widehat{DOB}=135^0\)

Ta có: \(\widehat{DOB}=\widehat{AOC}\)(hai góc đối đỉnh)

mà \(\widehat{DOB}=135^0\)

nên \(\widehat{AOC}=135^0\)

b: (2x+1):2=12:3

=>(2x+1):2=4

=>2x+1=2*4=8

=>2x=7

=>\(x=\dfrac{7}{2}\)

d: \(\dfrac{2x-14}{3}=\dfrac{12}{9}\)

=>\(\dfrac{2x-14}{3}=\dfrac{4}{3}\)

=>2x-14=4

=>2x=18

=>x=9

Gọi số cần tìm là: 3abc3

Ta có 3abc3 - abc = 37779

30000 + abc * 10 +3 - abc =37779

10abc - abc = 37779 - 30000 - 3

9abc = 7776

abc = 864 

Vậy số cần tìm là: 38643

a: tia OB nằm giữa hai tia OA và OC

=>\(\widehat{AOB}+\widehat{BOC}=\widehat{AOC}\)

=>\(\widehat{BOC}=165^0-20^0=145^0\)

b: Ta có: \(\widehat{BOC}+\widehat{COD}=180^0\)(hai góc kề bù)

=>\(\widehat{COD}+145^0=180^0\)

=>\(\widehat{COD}=35^0\)

ĐKXĐ: \(x\notin\left\{7;-1945\right\}\)

\(\dfrac{19x+8}{x-7}\cdot\dfrac{5x-9}{x+1945}+\dfrac{19x+8}{7-x}\cdot\dfrac{4x-2}{x+1945}\)

\(=\dfrac{19x+8}{x-7}\cdot\dfrac{5x-9}{x+1945}-\dfrac{19x+8}{x-7}\cdot\dfrac{4x-2}{x+1945}\)

\(=\dfrac{19x+8}{x-7}\cdot\dfrac{5x-9-4x+2}{x+1945}\)

\(=\dfrac{19x+8}{x+1945}\cdot\dfrac{x-7}{x-7}=\dfrac{19x+8}{x+1945}\)

Lời giải

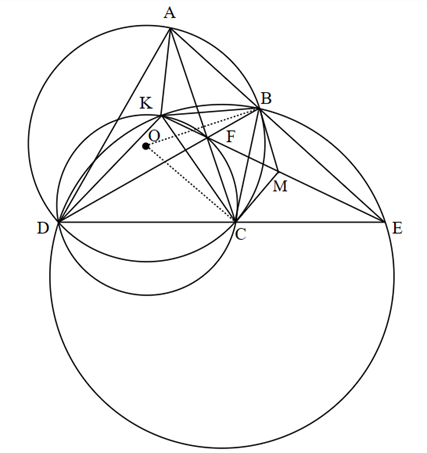
a) Vì điểm K nằm trên đường tròn ngoại tiếp ΔBDE nên tứ giác DKBE nội tiếp đường tròn

Suy ra $\widehat{BEK}=\widehat{BDK}$ (2 góc nội tiếp cùng chắn cung BK)

Hay $\widehat{AEK}=\widehat{FDK}$

Vì tứ giác DKFC nội tiếp đường tròn nên $\widehat{FCK}=\widehat{FDK}$

Suy ra $\widehat{AEK}=\widehat{FCK}$, hay $\widehat{AEK}=\widehat{ACK}$

Do đó tứ giác AKCE nội tiếp đường tròn

Suy ra $\widehat{KAE}+\widehat{KCE}={180}^{\circ }$

Mà $\widehat{KCD}+\widehat{KCE}={180}^{\circ }$ (hai góc kề bù)

Do đó $\widehat{KAE}=\widehat{KCD}$ hay $\widehat{KAB}=\widehat{KCD}$

Do tứ giác BKDE nội tiếp đường tròn nên $\widehat{KDE}+\widehat{KBE}={180}^{\circ }$

Mà $\widehat{KBA}+\widehat{KBE}={180}^{\circ }$ (hai góc kề bù)

Do đó $\widehat{KDE}=\widehat{KBA}$ hay $\widehat{KBA}=\widehat{KDC}$

Xét ΔDKC và ΔBKA có:

$\widehat{KBA}=\widehat{KDC}$ (chứng minh trên)

$\widehat{KAB}=\widehat{KCD}$ (chứng minh trên)

Suy ra (g.g)

Do đó $\frac{KC}{KA}=\frac{KD}{KB}$

Hay $\frac{KC}{KD}=\frac{KA}{KB}$

Ta có: $\widehat{BKD}=\widehat{DKC}+\widehat{BKC}$; $\widehat{AKC}=\widehat{BKA}+\widehat{BKC}$

Mà $\widehat{DKC}=\widehat{BKA}$, suy ra $\widehat{DKB}=\widehat{CKA}$

Xét ΔKBD và ΔKAC có:

$\widehat{DKB}=\widehat{CKA}$ (chứng minh trên)

$\frac{KC}{KD}=\frac{KA}{KB}$ (chứng minh trên)

Suy ra (c.g.c)

Do đó $\widehat{KBD}=\widehat{KAC}$

Hay $\widehat{KBF}=\widehat{KAF}$

Suy ra tứ giác AKFB nội tiếp đường tròn

Do đó $\widehat{BKF}=\widehat{BAF}$ (2 góc nội tiếp chắn cung BF)

Suy ra $\widehat{BKF}=\widehat{BAC}=\widehat{BDC}$ (do $\widehat{BAC},\widehat{BDC}$ cùng chắn cung BC)                   (1)

Ta có: $\widehat{BDC}=\widehat{FDC}=\widehat{FKC}$ (cùng chắn cung FC)                       (2)

Xét ΔBMC có $\widehat{MBC}+\widehat{MCB}+\widehat{BMC}={180}^{\circ }$ (tổng ba góc trong một tam giác)

Mà $\widehat{MBC}=\widehat{BAC},\widehat{MCB}=\widehat{BDC}$(Góc tạo bởi tiếp tuyến và dây cung)

Suy ra $\widehat{BAC}+\widehat{BDC}+\widehat{BMC}={180}^{\circ }$                                              (3)

Từ (1); (2) và (3) suy ra $\widehat{BKF}+\widehat{FKC}+\widehat{BMC}={180}^{\circ }$

Hay $\widehat{BKC}+\widehat{BMC}={180}^{\circ }$

Do đó tứ giác BKCM nội tiếp đường tròn

b) Ta có $\widehat{BKF}=\widehat{BDC}$ (chứng minh câu a)

Suy ra $\widehat{BKF}=\widehat{BDE}=\widehat{BKE}$ (Do tứ giác DKBE nội tiếp đường tròn)

Mà 2 điểm F và E nằm cùng phía so với BK

Suy ra 3 điểm K; F; E thẳng hàng

Hay F nằm trên KE                                                   (*)

Vì $\widehat{BKF}=\widehat{BAC},\widehat{CKF}=\widehat{BDC},\widehat{BAC}=\widehat{BDC}$

Nên $\widehat{BKF}=\widehat{CKF}$

Suy ra $\widehat{BKE}=\widehat{CKE}$ (Do K; F; E thẳng hàng)

Do đó KE là phân giác của $\widehat{BKC}$                     (4)

Xét (O) có MB, MC là 2 tiếp tuyến cắt nhau tại M

Nên MB = MC

Do đó tam giác MBC cân tại M

Suy ra $\widehat{MBC}=\widehat{MCB}$

Xét tứ giác BKCM nội tiếp đường tròn có $\widehat{MBC}=\widehat{MKC},\widehat{MCB}=\widehat{MKB}$

Suy ra $\widehat{MKC}=\widehat{MKB}$

Do đó KM là phân giác của $\widehat{BKC}$                                         (5)

Từ (4) và (5) suy ra 3 điểm K; M; E thẳng hàng hay M nằm trên KE (**)

Từ (*) và (**) suy ra 3 điểm E; M; F thẳng hàng

Vậy 3 điểm E; M; F thẳng hàng.

Ta có $x^2-y^2+4x-4y=\left(x-y\right)\left(x+y\right)+4\left(x-y\right)$

$=\left(x-y\right)\left(x+y+4\right).$

đây nhá cho mình đnx nha

người đó mua số kg là:

4x250+2x500=2000(g)=2kg

người đó mua số kg là:

4x250+2x500=2000(g)=2kg

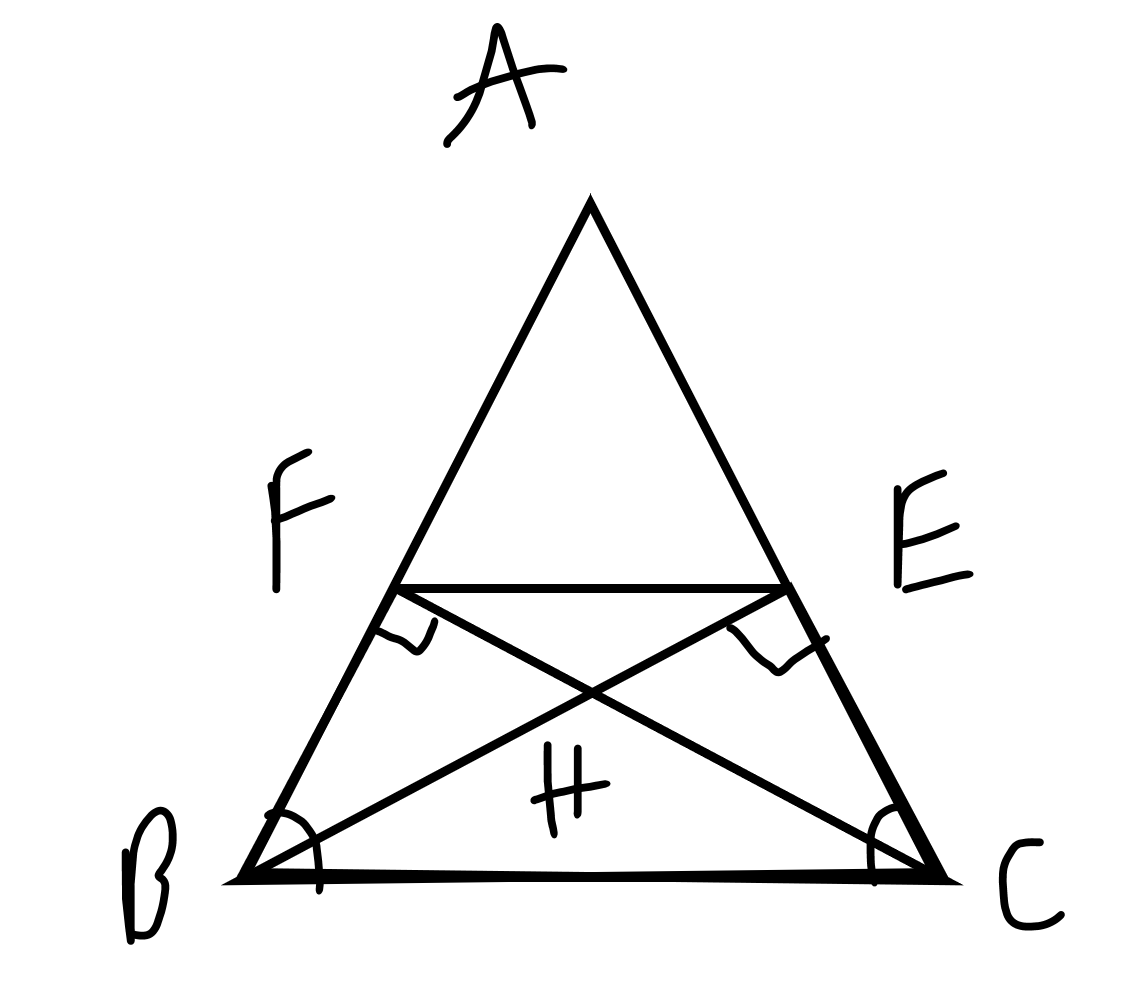
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có

AB=AC

\(\widehat{BAE}\) chung

Do đó: ΔAEB=ΔAFC

=>BE=CF

b: ΔAEB=ΔAFC

=>AE=AF

Xét ΔAFH vuông tại F và ΔAEH vuông tại E có

AH chung

AF=AE

Do đó: ΔAFH=ΔAEH

=>HE=HF

=>ΔHEF cân tại H

c: Xét ΔABC có \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)

nên EF//BC

d: Ta có: AE=AF

=>A nằm trên đường trung trực của EF(1)

Ta có: HE=HF

=>H nằm trên đường trung trực của EF(2)

Từ (1),(2) suy ra AH là đường trung trực của EF

=>AH\(\perp\)EF