tìm số tự nhiên n để phân số n+7/3n-1 có giá trị nguyên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Dùng phương pháp giải ngược
Giải:
20 trang của quyển truyện ứng với phân số là:
1 - (\(\dfrac{2}{5}\) + \(\dfrac{7}{15}\) + \(\dfrac{2}{3}\)) = - \(\dfrac{8}{15}\) (cuốn truyện)
- \(\dfrac{8}{15}\) < 0
Vậy không có cuốn truyện nào có số trang thỏa mãn đề bài.

Số đinh đã dùng chiếm:
\(\dfrac{5}{6}+\dfrac{1}{4}.\left(1-\dfrac{5}{6}\right)=\dfrac{21}{24}=\dfrac{7}{8}\) (tổng số đinh ốc)
Số đinh ốc chú Toàn có:
\(12:\left(1-\dfrac{7}{8}\right)=12:\dfrac{1}{8}=12.8=96\) (đinh ốc)

12 = 22.3
Ư(12) = {-12; -6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 12}
Lập bảng ta có:
| 2\(x\) + 1 | -12 | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | 12 |
| \(x\) | -\(\dfrac{13}{2}\) | -\(\dfrac{7}{2}\) | -\(\dfrac{5}{2}\) | -2 | -\(\dfrac{3}{2}\) | -1 | 0 | \(\dfrac{1}{2}\) | 1 | \(\dfrac{3}{2}\) | \(\dfrac{5}{2}\) | -\(\dfrac{11}{2}\) |
| y - 5 | -4 | -12 | 12 | 4 | ||||||||
| y | 1 | -7 | 17 | 9 | ||||||||
| \(x;y\in\)Z | loại | loại | loại | loại | loại | loại | loại | loại |
Theo bảng trên ta có các cặp \(x;y\) nguyên thỏa mãn đề bài là:
(\(x;y\)) = (-2; 1); (-1; -7);(0; 17); (1; 9)

Bài 1:
a; Cứ 1 điểm sẽ tạo với 25 - 1 điểm còn lại 25 - 1 đường thẳng
Với 25 điểm sẽ tạo được số đường thẳng là: (25 - 1)x25
Theo cách tính trên mội đường thẳng được tính hai lần
Vậy thực tế số đường thẳng tạo được là:
(25 - 1) x 25 : 2 = 300 (đường thẳng)
Kết luận với 25 điểm trong đó không có ba điểm nào thẳng hàng thì sẽ tạo được 300 đường thẳng.
Bài 1
C; Số điểm mà trong đó bất cứ 3 điểm nào cũng không thẳng hàng với nhau là:
25 - 8 = 17 (điểm)
Xét 17 điểm đó ta có:
Cứ một điểm sẽ tạo được với 17 - 1 điểm còn lại 17 - 1 đường thẳng
Với 17 điểm sẽ tạo được (17- 1)x17 đường thẳng
Theo cách tính trên mỗi đường thẳng được tính hai lần nên thực tế số đường thẳng tạo được là:
(17 - 1).17 : 2 = 136 (đường thẳng)
Vét 8 điểm thẳng hàng thì sẽ tạo được số đường thẳng là 1 đường thẳng đó là đường thẳng d
Xét 17 điểm nằm ngoài đường thẳng d ta có
Cứ một điểm sẽ tạo với 8 điểm trên đường thẳng d là 8 đường thẳng
Với 17 điểm sẽ tạo được số đường thẳng là:
17 x 8 = 136 (đường thẳng)
Từ các lập luận trên ta có tất cả số đường thẳng được tạo sẽ là:
136 + 1 + 136 = 273 (đường thẳng)
Kết luận:...

Coi so cam mà bác Long mang đi là 1 đơn vị.
Sau khi bán buổi sáng Bác Long còn lại số cam là:
1-\(\dfrac{2}{5}\)=\(\dfrac{3}{5}\) (số cam)
Buổi chiều Bác Long bán được số phần cam ban đầu là:
\(\dfrac{3}{5}\).\(\dfrac{1}{3}\)=\(\dfrac{1}{5}\) (số cam)
24 quả chiếm số phần cam ban đầu là:
\(\dfrac{3}{5}-\dfrac{1}{5}\)=\(\dfrac{2}{5}\) (số cam)
Bác Long mang đi số quả cam là:
\(24:\dfrac{2}{5}\)=60 (quả cam)
Đáp số: 60 quả cảm
24 quả ứng với phân số là: 1 - \(\dfrac{1}{3}\) = \(\dfrac{2}{3}\) (số cam còn lại sau buổi sáng)
Số cam còn lại sau buổi sáng là: 24 : \(\dfrac{2}{3}\) = 36 (quả)
36 quả ứng với phân số là: 1 - \(\dfrac{2}{5}\) = \(\dfrac{3}{5}\) (số cam mang đi)
Số cam mang đi là: 36 : \(\dfrac{3}{5}\) = 60 (quả)
Kết luận: Số cam bác Long mang đi bán là 60 quả.

\(N=\dfrac{-7}{10^{2005}}+\dfrac{-15}{10^{2006}}\)
\(=\dfrac{-7\cdot10+\left(-15\right)}{10^{2006}}=\dfrac{-85}{10^{2006}}\)
\(M=\dfrac{-15}{10^{2005}}+\dfrac{-7}{10^{2006}}\)
\(=\dfrac{-15\cdot10+\left(-7\right)}{10^{2006}}=\dfrac{-157}{10^{2006}}\)
Vì -85>-157
nên \(-\dfrac{85}{10^{2006}}>-\dfrac{157}{10^{2006}}\)
=> N>M

Đây là dạng toán nâng cao chuyên đề tìm một số khi biết giá trị phân số của nó. Cấu trúc thi chuyên, thi học sinh giỏi. Hôm nay olm.vn sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp giải ngược như sau:
Giải:
24 quả ứng với phân số là:
1 - \(\dfrac{1}{3}\) = \(\dfrac{2}{3}\) (số cam còn lại sau lần bán buổi chiều)
Số cam còn lại sau lần bán buổi chiều là:
24 : \(\dfrac{2}{3}\) = 36 (quả cam)
36 quả cam ứng với phân số là:
1 - \(\dfrac{2}{5}\) = \(\dfrac{3}{5}\) (số cam)
Số cam bác Long mang đi bán là:
36 : \(\dfrac{3}{5}\) = 60 (quả)
Đáp số: 60 quả

Trong tháng hai tổ đó làm được:
\(\dfrac{5}{16}\) - \(\dfrac{1}{24}\) = \(\dfrac{13}{48}\) (công việc)
Trong tháng ba tổ đó làm được:
\(\dfrac{13}{48}\) + \(\dfrac{1}{12}\) = \(\dfrac{17}{48}\)(công việc)
Tháng tư tổ đó làm được:
1 - \(\dfrac{5}{16}\) - \(\dfrac{13}{48}\) - \(\dfrac{17}{48}\) = \(\dfrac{1}{16}\) (công việc)
Kết luận:..
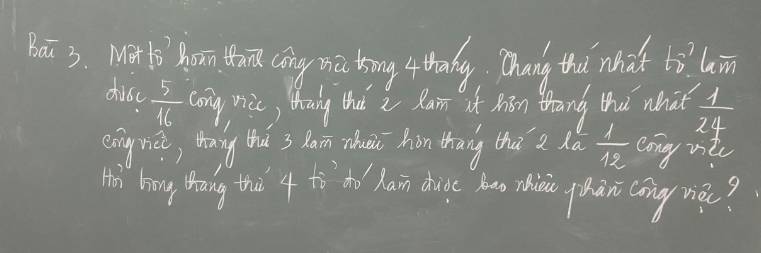
ĐKXĐ: \(n\ne\dfrac{1}{3}\)
Để \(\dfrac{n+7}{3n-1}\in Z\) thì \(n+7⋮3n-1\)
=>\(3n+21⋮3n-1\)
=>\(3n-1+22⋮3n-1\)
=>\(3n-1\inƯ\left(22\right)\)
=>\(3n-1\in\left\{1;-1;2;-2;11;-11;22;-22\right\}\)
=>\(3n\in\left\{2;0;3;-1;12;-10;23;-21\right\}\)
=>\(n\in\left\{\dfrac{2}{3};0;1;-\dfrac{1}{3};4;-\dfrac{10}{3};\dfrac{23}{3};-7\right\}\)
mà n là số tự nhiên
nên \(n\in\left\{0;1;4\right\}\)
Ta có: \(\dfrac{n+7}{3n-1}\in Z\Rightarrow\dfrac{3\left(n+7\right)}{3n-1}\in Z\)
\(\dfrac{3\left(n+7\right)}{3n-1}=\dfrac{3n+21}{3n-1}=\dfrac{3n-1+22}{3n-1}=1+\dfrac{22}{3n-1}\)
⇒ 22 ⋮ 3n + 1
⇒ 3n - 1 ∈ Ư(22)={1; -1; 2; -2; 11; -11; 22; -22}
⇒ 3n ∈ {2; 0; 3; -1; 12; -10; 23; -21}
⇒ n ∈ \(\left\{\dfrac{2}{3};0;1;-\dfrac{1}{3};4;-\dfrac{10}{3};\dfrac{23}{3};-7\right\}\)
Mà: n ∈ N
\(\Rightarrow n\in\left\{0;1;4;7\right\}\)