
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Em nên viết bằng công thức toán học có biểu tượng Σ góc trái màn hình em nhé. Như vậy mọi người mới hiểu đúng đề được để có thể hỗ trợ tốt nhất cho em.

Ta có:
\(x^2-y^2-4x-25=0\\\Leftrightarrow (x^2-4x+4)-y^2-29=0\\\Leftrightarrow (x-2)^2-y^2=29\\\Leftrightarrow (x-y-2)(x+y-2)=29\)
Vì x, y nguyên nên \(x-y-2;x+y-2\) có giá trị nguyên
\(\Rightarrow x-y-2;x+y-2\) là các ước của 29
Ta có bảng sau:
| x - y - 2 | 1 | 29 | -1 | -29 |
| x + y - 2 | 29 | 1 | -29 | -1 |
| x | 17 | 17 | -13 | -13 |
| y | 14 | -14 | -14 | 14 |
Vì các giá trị tìm được đều thoả mãn x, y nguyên nên \((x;y)=(17;14);(17;-14);(-13;-14);(-13;14)\)
$Toru$

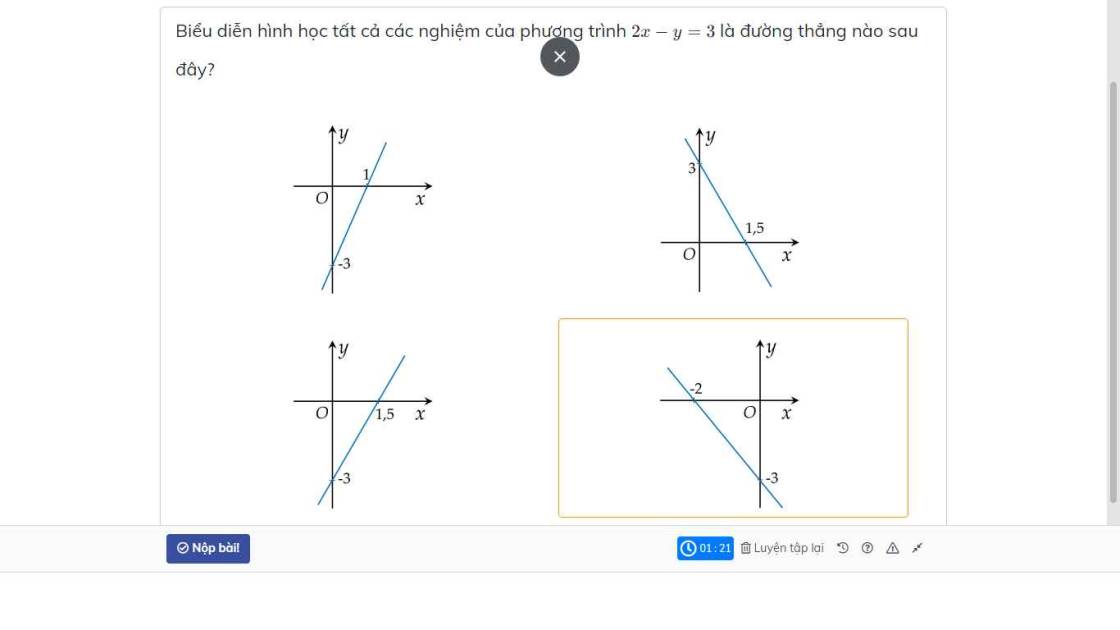
Ta có pt: $2x-y=3$ (1)
+, $y=0\Rightarrow 2x=3\Leftrightarrow x=1,5$
$\Rightarrow (1,5;0)$ là giao điểm của pt (1) với trục hoành
+, $x=0\Rightarrow -y=3\Leftrightarrow y=-3$
$\Rightarrow (0;-3)$ là giao điểm của pt (1) với trục tung
Kẻ đường thẳng đi qua hai điểm trên, ta được đường thẳng biểu diễn các nghiệm của pt $2x-y=3$
$\Rightarrow$ Chọn đáp án:


2:
\(\text{Δ}=\left[-\left(2m-1\right)\right]^2-4\cdot1\cdot\left(m^2-m-2\right)\)
\(=4m^2-4m+1-4m^2+4m+8=9>0\)
=>Phương trình luôn có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{2m-1-\sqrt{9}}{2}=\dfrac{2m-1-3}{2}=m-2\\x=\dfrac{2m-1+3}{2}=\dfrac{2m+2}{2}=m+1\end{matrix}\right.\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m-1\\x_1x_2=\dfrac{c}{a}=m^2-m-2\end{matrix}\right.\)
\(\dfrac{x_1^4+x_1^3+m^2-m-2}{x_1}-\dfrac{x_2^4+x_2^3+m^2-m-2}{x_2}=-7m^2+4m+24\)
=>\(x_1^3+x_1^2+\dfrac{x_1x_2}{x_1}-x_2^3-x_2^2-\dfrac{x_1x_2}{x_2}=-7m^2+4m+24\)
=>\(\left(x_1^3-x_2^3\right)+\left(x_1^2-x_2^2\right)+\left(x_2-x_1\right)=-7m^2+4m+24\)
=>\(\left(x_1-x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)+\left(x_1-x_2\right)\left(x_1+x_2\right)-\left(x_1-x_2\right)=-7m^2+4m+24\)
=>)\(\left(x_1-x_2\right)\left(x_1^2+x_2x_1+x_2^2+x_1+x_2-1\right)=-7m^2+4m+24\)(1)
TH1: \(x_1=m-2;x_2=m+1\)
(1) sẽ tương đương với:
\(\left(m-2-m-1\right)\left[\left(m-2\right)^2+\left(m-2\right)\left(m+1\right)+\left(m+1\right)^2+m-2+m+1-1\right]=-7m^2+4m+24\)
=>\(-3\left[m^2-4m+4+m^2-m-2+m^2+2m+1+2m-2\right]=-7m^2+4m+24\)
=>\(-3\left(3m^2-m+1\right)+7m^2-4m-24=0\)
=>\(-9m^2+3m-3+7m^2-4m-24=0\)
=>\(-2m^2-m-27=0\)
=>\(m\in\varnothing\)
TH2: \(x_1=m+1;x_2=m-2\)
(1) sẽ trở thành:
\(\left(m+1-m+2\right)\left[\left(m+1\right)^2+\left(m+1\right)\left(m-2\right)+\left(m-2\right)^2+2m-1-1\right]=-7m^2+4m+24\)
=>\(3\left(m^2+2m+1+m^2-m-2+m^2-4m+4+2m-2\right)=-7m^2+4m+24\)
=>\(3\left(3m^2-m+1\right)+7m^2-4m-24=0\)
=>\(9m^2-3m+3+7m^2-4m-24=0\)
=>\(16m^2-7m-21=0\)
=>\(m=\dfrac{7\pm\sqrt{1393}}{32}\)

2:
\(\text{Δ}=\left[-\left(2m-1\right)\right]^2-4\cdot1\cdot\left(m^2-m-2\right)\)
\(=4m^2-4m+1-4m^2+4m+8=9>0\)
=>Phương trình luôn có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{2m-1-\sqrt{9}}{2}=\dfrac{2m-1-3}{2}=m-2\\x=\dfrac{2m-1+3}{2}=\dfrac{2m+2}{2}=m+1\end{matrix}\right.\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m-1\\x_1x_2=\dfrac{c}{a}=m^2-m-2\end{matrix}\right.\)
\(\dfrac{x_1^4+x_1^3+m^2-m-2}{x_1}-\dfrac{x_2^4+x_2^3+m^2-m-2}{x_2}=-7m^2+4m+24\)
=>\(x_1^3+x_1^2+\dfrac{x_1x_2}{x_1}-x_2^3-x_2^2-\dfrac{x_1x_2}{x_2}=-7m^2+4m+24\)
=>\(\left(x_1^3-x_2^3\right)+\left(x_1^2-x_2^2\right)+\left(x_2-x_1\right)=-7m^2+4m+24\)
=>\(\left(x_1-x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)+\left(x_1-x_2\right)\left(x_1+x_2\right)-\left(x_1-x_2\right)=-7m^2+4m+24\)
=>)\(\left(x_1-x_2\right)\left(x_1^2+x_2x_1+x_2^2+x_1+x_2-1\right)=-7m^2+4m+24\)(1)
TH1: \(x_1=m-2;x_2=m+1\)
(1) sẽ tương đương với:
\(\left(m-2-m-1\right)\left[\left(m-2\right)^2+\left(m-2\right)\left(m+1\right)+\left(m+1\right)^2+m-2+m+1-1\right]=-7m^2+4m+24\)
=>\(-3\left[m^2-4m+4+m^2-m-2+m^2+2m+1+2m-2\right]=-7m^2+4m+24\)
=>\(-3\left(3m^2-m+1\right)+7m^2-4m-24=0\)
=>\(-9m^2+3m-3+7m^2-4m-24=0\)
=>\(-2m^2-m-27=0\)
=>\(m\in\varnothing\)
TH2: \(x_1=m+1;x_2=m-2\)
(1) sẽ trở thành:
\(\left(m+1-m+2\right)\left[\left(m+1\right)^2+\left(m+1\right)\left(m-2\right)+\left(m-2\right)^2+2m-1-1\right]=-7m^2+4m+24\)
=>\(3\left(m^2+2m+1+m^2-m-2+m^2-4m+4+2m-2\right)=-7m^2+4m+24\)
=>\(3\left(3m^2-m+1\right)+7m^2-4m-24=0\)
=>\(9m^2-3m+3+7m^2-4m-24=0\)
=>\(16m^2-7m-21=0\)
=>\(m=\dfrac{7\pm\sqrt{1393}}{32}\)

Giả sử x+y=0
=>x=-y
\(\left(\sqrt{x^2+3}+x\right)\left(\sqrt{y^2+3}+y\right)\)
\(=\left(\sqrt{\left(-y\right)^2+3}-y\right)\left(\sqrt{y^2+3}+y\right)\)
\(=\left(\sqrt{y^2+3}-y\right)\left(\sqrt{y^2+3}+y\right)\)
\(=y^2+3-y^2=3\)(Đúng với Giả thiết)
=>ĐPCM

Gọi chữ số hàng chục là: a
Chữ số hàng đơn vị là: b
ĐK: \(1\le a\le9;0\le b\le9\)
Khi đó ta có: \(a-b=5\) (1)
Số đó có dạng: \(\overline{ab}=10a+b\)
Số đó chia cho tổng hai chữ số của nó được thương là 7 và dư 6 nên ta có pt:
\(\Rightarrow10a+b=7\left(a+b\right)+6\)
\(\Leftrightarrow10a+b=7a+7b+6\)
\(\Leftrightarrow3a-6b=6\Leftrightarrow a-2b=3\left(2\right)\)
Từ (1) và (2) ta có hpt:
\(\left\{{}\begin{matrix}a-b=5\\a-2b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=2\end{matrix}\right.\) (tm)
Vậy số cần tìm là 72

tham khảo nhé
Giả sử 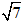
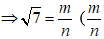
Điều này chứng tỏ m2 ⋮ 7 mà 7 là số nguyên tố nên m ⋮ 7
Đặt m = 7k (k ∈ Z), suy ra m2 = (7k)2 = 49k2 (2)
Từ (1) và (2) suy ra: 7n2 = 49k2 ⇒ n2 = 7k2
⇒ n2 ⋮ 7 ⇒ n ⋮ 7 (vì 7 là số nguyên tố)
Do đó cả m và n đều cùng chia hết cho 7, vậy 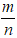
Vậy giả sử sai nên 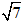

Ta có \(x+y+xy=3\Leftrightarrow-xy=x+y-3\). Khi đó \(P=\dfrac{3}{x+y}+x+y-3\)
Đặt \(x+y=t\left(t>0\right)\). Khi đó: \(P=\dfrac{3}{t}+t-3\)
Lại có \(xy\le\dfrac{\left(x+y\right)^2}{4}\) \(\Leftrightarrow3=x+y+xy\le\left(x+y\right)+\dfrac{\left(x+y\right)^2}{4}\) \(=t+\dfrac{t^2}{4}\)
\(\Leftrightarrow t^2+4t\ge12\) \(\Leftrightarrow t\ge2\)
Khi đó \(P=\dfrac{3}{t}+t-3=\dfrac{3}{t}+\dfrac{3}{4}t+\dfrac{t}{4}-3\)
\(\ge2\sqrt{\dfrac{3}{t}.\dfrac{3}{4}t}+\dfrac{2}{4}-3\) (chú ý rằng \(t\ge2\))
\(=2.\dfrac{3}{2}+\dfrac{1}{2}-3\)
\(=\dfrac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}t=2\\\dfrac{3}{t}=\dfrac{3}{4}t\end{matrix}\right.\Leftrightarrow t=2\) \(\Leftrightarrow x+y=2\) \(\Rightarrow xy=1\)
\(\Rightarrow x=y=1\)
Vậy \(minP=\dfrac{1}{2}\) khi \(x=y=1\)


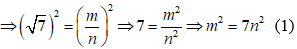
Bài 2:
a: \(\sqrt{\left(2x-1\right)^2}=4\)
=>|2x-1|=4
=>\(\left[{}\begin{matrix}2x-1=4\\2x-1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
b: ĐKXĐ: x>=-1
\(\sqrt{4x+4}-\sqrt{9x+9}-8\sqrt{\dfrac{x+1}{16}}=5\)
=>\(2\sqrt{x+1}-3\sqrt{x+1}-8\cdot\dfrac{\sqrt{x+1}}{4}=5\)
=>\(-3\sqrt{x+1}=5\)
=>\(\sqrt{x+1}=-\dfrac{5}{3}\)(vô lý)
=>Phương trình vô nghiệm
Bài 3:
a: \(Q=\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2}{\sqrt{x}+1}-\dfrac{2}{x-1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2}{\sqrt{x}+1}-\dfrac{2}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)-2\left(\sqrt{x}-1\right)-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x+\sqrt{x}-2\sqrt{x}+2-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
b: Thay x=9 vào Q, ta được:
\(Q=\dfrac{3}{3+1}=\dfrac{3}{4}\)
Bài 4:
\(\sqrt{x-2\sqrt{x-1}}+\sqrt{x+2\sqrt{x-1}}\)
\(=\sqrt{x-1-2\sqrt{x-1}+1}+\sqrt{x-1+2\sqrt{x-1}+1}\)
\(=\sqrt{\left(\sqrt{x-1}-1\right)^2}+\sqrt{\left(\sqrt{x-1}+1\right)^2}\)
\(=\sqrt{x-1}-1+\sqrt{x-1}+1\left(x>=2\right)\)
\(=2\sqrt{x-1}\)
Cứu câu 2,3,4 đề 2 vs ạ