Tìm các số thực x,y thỏa mãn: \(2x+y^2-2y\sqrt{x-1}+2\sqrt{x-1}-4y+3=0\)(1000% ko sai đề)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) √x=3⇒x=32⇒x=9x=3⇒x=32⇒x=9
b) √x=√5⇒x=(√5)2⇒x=5x=5⇒x=(5)2⇒x=5
c) √x=0⇒x=02⇒x=0x=0⇒x=02⇒x=0
d) Căn bậc 2 số học là số không âm nên không tồn tại giá trị nào của x thỏa mãn √x=–2.x=–2.

1, \(A=\frac{\sqrt{x}-3}{\sqrt{x}+2};\)khi \(x=25\)
\(\Rightarrow A=\frac{\sqrt{25}-3}{\sqrt{25}+2}=\frac{5-3}{5+2}=\frac{2}{7}\)
2, \(B=\left(\frac{1}{\sqrt{x}-2}+\frac{x-2}{x-4}\right):\frac{\sqrt{x}}{\sqrt{x}-2},\)\(x>0,x\ne4\)
\(=\left(\frac{\sqrt{x}+2+x-2}{x-4}\right):\frac{\sqrt{x}}{\sqrt{x}-2}\)
\(=\frac{\sqrt{x}+x}{x-4}.\frac{\sqrt{x}-2}{\sqrt{x}}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+1\right).\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right).\sqrt{x}}=\frac{\sqrt{x}+1}{\sqrt{x}+2}\left(đpcm\right)\)

\(a=\sqrt{2+\sqrt{2+\sqrt{2}}}< \sqrt{2+\sqrt{2+\sqrt{4}}}\)
\(=\sqrt{2+\sqrt{2+2}}=\sqrt{2+2}=2\)


Trước tiên ta chứng minh:
\(x\sqrt{x}-3\sqrt{x}+3>0\)
\(\Leftrightarrow\left(x\sqrt{x}-2x+\sqrt{x}\right)+\left(2x-4\sqrt{x}+2\right)+1>0\)
\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}-1\right)^2+2\left(\sqrt{x}-1\right)^2+1>0\)(đúng )
\(\Rightarrow A=\frac{\sqrt{x}}{x\sqrt{x}-3\sqrt{x}+3}\ge0\)
Ta chứng minh:
\(A=\frac{\sqrt{x}}{x\sqrt{x}-3\sqrt{x}+3}< 2\)
\(\Leftrightarrow2x\sqrt{x}-6\sqrt{x}+6-\sqrt{x}>0\)
\(\Leftrightarrow2x\sqrt{x}-7\sqrt{x}+6>0\)
\(\Leftrightarrow\left(2x\sqrt{x}-4x+2\right)+\left(4x-\frac{2.2.7}{4}\sqrt{x}+\frac{49}{16}\right)+\frac{47}{16}>0\)
\(\Leftrightarrow2\sqrt{x}\left(\sqrt{x}-1\right)^2+\left(2\sqrt{x}-\frac{7}{2}\right)^2+\frac{47}{16}>0\)(đúng )
Từ đây ta được: \(0\le A< 1\)
\(\Rightarrow A=\left\{0;1\right\}\)
Thế A vô tìm x nha. Cái nào thỏa mãn thì lụm không thì bỏ nha.

\(\left(1+tanx\right)\left(1+cotx\right)-2=1+cotx+tanx+tanx.cotx-2\)
\(=1+\frac{cosx}{sinx}+\frac{sinx}{cosx}+1-2=\frac{cos^2x+sin^2x}{sinx.cosx}\)
\(=\frac{1}{\frac{3}{4}}=\frac{4}{3}\)


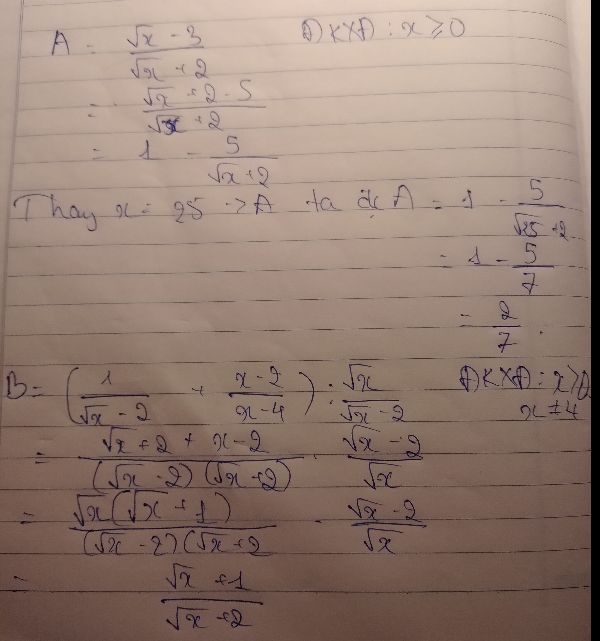

\(2\left(2x+y^2-2y\sqrt{x-1}+2\sqrt{x-1}-4y+3\right)=0\)
Ta có:
\(VT=\left(y-1\right)^2-4\sqrt{x-1}\left(y-1\right)+4\left(x-1\right)+y^2-6y+9\)
\(=\left[\left(y-1\right)-2\sqrt{x-1}\right]^2+\left(y-3\right)^2\ge0=VP\)
Dấu = xảy ra khi:
\(\hept{\begin{cases}y-3=0\\y-1=2\sqrt{x-1}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=3\\x=2\end{cases}}\)