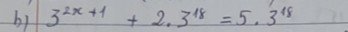
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=2021-\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2021.2022}=\right)\)
\(=2021-\left(\dfrac{2-1}{1.2}+\dfrac{3-2}{2.3}+\dfrac{4-3}{3.4}+...+\dfrac{2022-2021}{2021.2022}\right)=\)
\(=2021-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\right)=\)
\(=2021-\left(1-\dfrac{1}{2022}\right)=2021-\dfrac{2021}{2022}\)

a: Các cặp tia đối nhau gốc A là:
AB,Ax
AO,Ax
Ay,Ax
b: Trên tia Ay, ta có: AO<AB(3cm<6cm)
nên O nằm giữa A và B
=>AO+OB=AB
=>OB+3=6
=>OB=3(cm)
c: Vì O nằm giữa A và B
và OA=OB(=3cm)
nên O là trung điểm của AB
a) Cặp tia đối nhau gốc A trên hình vẽ là tia OA và tia AO.
b) Độ dài đoạn thẳng OB có thể tính bằng cách sử dụng định lý Pythagoras trong tam giác vuông OAB:
OB² = OA² + AB²
OB² = 3² + 6²
OB² = 9 + 36
OB² = 45
OB = √45 ≈ 6.71 cm
c) Điểm O không phải là trung điểm của đoạn thẳng AB. Để chứng minh điều này, ta có thể tính độ dài của OA và OB:
OA = 3 cm
OB = 6.71 cm
Ta thấy OA ≠ OB, do đó O không là trung điểm của AB.
tick mik nha

a/
BC=AB-AC=4-1=3 cm
b/
CD=BC+BD
Mà BC=BD=3cm
=> CD = 3+3=6 cm

Vì điểm M nằm giữa 2 điểm O và N nên ta có:
⇔ OM + MN = ON
Thay số : 3 + MN = 7
MN = 7 - 3
⇔ MN= 4 cm.
Vì A là trung điểm của MN nên ta có:
⇔ MA = AN = MN/2
Thay số : MA = AN = 4/2 = 2cm
⇔ Điểm M nằm giữa 2 điểm O và A nên ta có:
⇔ OM + MA = OA
Thay số : 3 + 2 = OA
⇔ OA = 5cm.
Vậy OA = 5cm.

`@` `\text {Ans}`
`\downarrow`
\(\left(\dfrac{3}{5}\right)^{2x-1}=\left(\dfrac{9}{25}\right)^3\)
`=>`\(\left(\dfrac{3}{5}\right)^{2x-1}=\left(\dfrac{3^2}{5^2}\right)^3\)
`=>`\(\left(\dfrac{3}{5}\right)^{2x-1}=\left(\dfrac{3}{5}\right)^6\)
`=> 2x - 1 = 6`
`=> 2x=6+1`
`=> 2x=7`
`=> x = 7/2`
`=> x = 3,5`
Vậy, `x = 3,5`
`@` `\text {Kaizuu lv uuu}`

`@` `\text {Ans}`
`\downarrow`
Ta có:
\(5^{333}=\left(5^3\right)^{111}=125^{111}\)
\(11^{222}=\left(11^2\right)^{111}=121^{111}\)
Vì `125 > 121 =>`\(125^{111}>121^{111}\)
`=>`\(5^{333}>11^{222}\)
Vậy, \(5^{333}>11^{222}\)
_____
`@` So sánh lũy thừa cùng cơ số:
Nếu `m > n =>`\(a^m>a^n\left(m,n\ne0,a>1\right)\)
`@` So sánh lũy thừa cùng số mũ:
Nếu `a > b =>`\(a^m>b^m\left(a,b>1,m\ne0\right)\)
`@` `\text {Kaizuu lv uuu}`

`3/7 +1/2 -17/7 +3/2`
`= ( 3/7 -17/7) +(1/2 +3/2)`
`= -14/7 + 4/2`
`= -2 + 2`
`=0`
`@` `\text {Ans}`
`\downarrow`
\(\dfrac{3}{7}+\dfrac{1}{2}-\dfrac{17}{7}+\dfrac{3}{2}\)
`=`\(\left(\dfrac{3}{7}-\dfrac{17}{7}\right)+\left(\dfrac{1}{2}+\dfrac{3}{2}\right)\)
`=`\(-\dfrac{14}{7}+\dfrac{4}{2}\)
`= -2+2=0`

`@` `\text {Ans}`
`\downarrow`
`5/4 - (-3 1/2) - 7/10`
`= 5/4 + 3 1/2 - 7/10`
`= 5/4 + 7/2 - 7/10`
`= 1,25 + 3,5 - 0,7`
`= 4,75 - 0,7`
`= 4,05`

\(\Leftrightarrow3^{2x+1}=3.3^{18}=3^{19}\)
\(\Rightarrow2x+1=19\)
\(\Leftrightarrow2x=18\Leftrightarrow x=9\)