Cho đường tròn (O) và điểm P nằm ngoài (O). Hai tiếp tuyến PA, PB (A, B là các tiếp điểm), trên tia đối tia BP lấy điểm M. Đường tròn ngoại tiếp tam giác APM cắt (O) tại điểm thứ hai D. Gọi H là hình chiếu của B lên AM. CMR \(\widehat{HDM}=2\widehat{AMP}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 9:
Để \(A\) giao \(B\) là tập số thực thì
\(\left\{{}\begin{matrix}1-m\le-3\\\dfrac{m+3}{2}\ge3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge4\\m\ge3\end{matrix}\right.\Leftrightarrow m\ge4\).

Lời giải:
Ta có: A ⊂ B , nên A ∪ X = B khi X là tập hợp con của B chứa ít nhất 3 phần tử 1, 3 và 4 . Vậy ta có 4 tập hợp X là: {1 ; 3 ; 4}, {0 ; 1 ; 3 ; 4}, {2 ; 1 ; 3 ; 4}, {0 ; 2 ; 1 ; 3 ; 4} .

Giả sử tồn tại số tự nhiên \(n\) để \(P=n^2+15n+48⋮121\). Khi đó do \(121=11^2\) nên \(P⋮11\)
Mà \(P=n^2+15n+48=n^2+2n+13n+26+22\) \(=n\left(n+2\right)+13\left(n+2\right)+22\) \(=\left(n+2\right)\left(n+13\right)+22\)
Ta có \(P⋮11\) (g/s) và \(22⋮11\), từ đó \(\left(n+2\right)\left(n+13\right)⋮11\). Hơn nữa 11 là số nguyên tố nên trong 2 số \(n+2\) và \(n+13\) sẽ luôn có một số chia hết cho 11.
Nếu \(n+2⋮11\) thì hiển nhiên \(n+13=n+2+11⋮11\), do đó \(\left(n+2\right)\left(n+13\right)⋮11.11=121\), mà \(P=\left(n+2\right)\left(n+13\right)+22⋮121\) nên \(22⋮121\), đây rõ ràng là một điều vô lý. Vậy điều giả sử là sai \(\Rightarrow\) với mọi số tự nhiên \(n\) thì \(n^2+15n+48⋮̸121\)
À đoạn cuối mình bổ sung thêm là nếu \(n+13⋮11\) thì \(n+2=n+13-11⋮11\) nên \(\left(n+2\right)\left(n+13\right)⋮121\) và cũng dẫn đến điều vô lí nữa nhé.

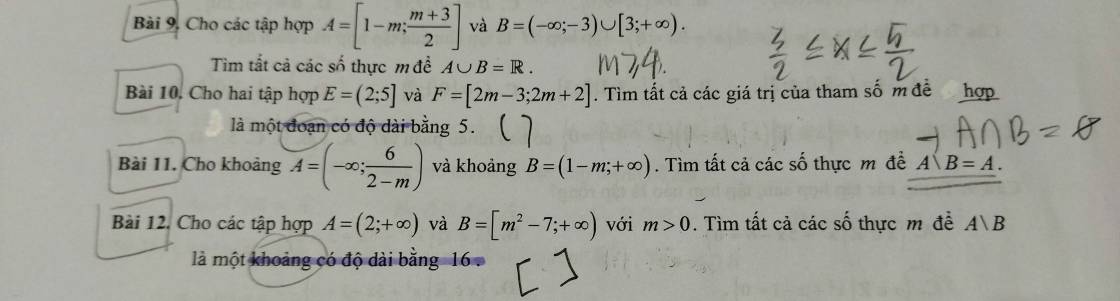

tính nhanh (1-1/17)*(1-2/17)*(1-3/17)*...*(1-10/17)