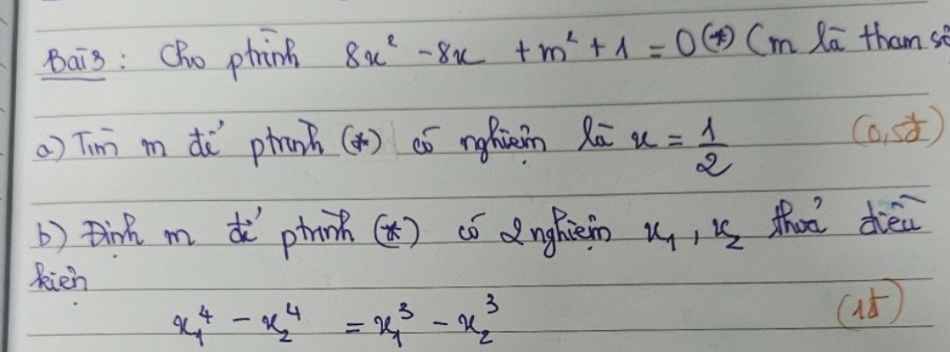Lời giải:

$\Delta' (*) = 4^2-8(m^2+1)=8-8m^2$

Để pt có 2 nghiệm $x_1,x_2$ thì:

$\Delta'(*) = 8-8m^2\geq 0\Leftrightarrow 1-m^2\geq 0$

$\Leftrightarrow -1\leq m\leq 1$

Áp dụng định lý Viet:

$x_1+x_2=1$

$x_1x_2=\frac{m^2+1}{8}$
Khi đó:

$x_1^4-x_2^4=x_1^3-x_2^3$
$\Leftrightarrow (x_1^2-x_2^2)(x_1^2+x_2^2)=(x_1-x_2)(x_1^2+x_1x_2+x_2^2)$

$\Leftrightarrow (x_1-x_2)[(x_1+x_2)(x_1^2+x_2^2)-(x_1^2+x_1x_2+x_2^2)]=0$

$\Leftrightarrow (x_1-x_2)[1(x_1^2+x_2^2)-(x_1^2+x_1x_2+x_2^2)]=0$

$\Leftrightarrow (x_1-x_2)(-x_1x_2)=0$

$\Leftrightarrow (x_1-x_2).\frac{-(m^2+1)}{8}=0$

$\Leftrightarrow x_1-x_2=0$ (do $m^2+1\geq 1>0$ với mọi $m$ nên số này khác 0)

$\Leftrightarrow x_1=x_2$
Kết hợp $x_1+x_2=1$

$\Rightarrow x_1=x_2=\frac{1}{2}$

$\frac{m^2+1}{8}=x_1x_2=\frac{1}{4}$

$\Leftrightarrow m^2+1=2$

$\Leftrightarrow m^2=1\Leftrightarrow m=\pm 1$ (tm)

3,24 x \(x\) - 2,4 x 0,38  = 21,12

3,24 x \(x\) - 0,912 = 21,12

3,24 x \(x\)             = 21,12 + 0,912

3,24 x \(x\)            =  22,032

          \(x\)            = 22,032 : 3,24

           \(x\)          = 6,8 

3,24 x X - 2,4 x 0,38 = 21,12

3,24 x X - 0,912 = 21,12

3,24 x X = 21,12 + 0,912

3,24 x X = 22,032

           X = 22,032 : 3,24

           X = 6,8

Lời giải:

$BC=\sqrt{AB^2+AC^2}=\sqrt{18^2+24^2}=30$ (cm) - áp dụng định lý Pitago.

Nửa chu vi tam giác: $p=(AB+BC+AC):2=(18+24+30):2=36$ (cm) 

Diện tích: $S=AB.AC:2=18.24:2=216$ (cm²)

Áp dụng công thức:
$S=pr$ với $r$ là bán kính đường tròn nội tiếp tam giác.

$r=\frac{S}{p}=\frac{216}{36}=6$ (cm)

Lời giải:

$A=\frac{(2011\times 2022+2011)+2023\times 11}{2022\times (2021-2020)}$
$=\frac{2011\times(2022+1)+2023\times 11}{2022\times 1}$
$=\frac{2011\times 2023+2023\times 11}{2022}$

$=\frac{2023\times (2011+11)}{2022}=\frac{2023\times 2022}{2022}=2023$

10 cây kem giá tiền là :

\(5000\times10=50000\left(đ\right)\)

Đáp số : 50000 đ

5000x10=50000(đồng)

Lời giải:

Gọi số bị trừ là $a$ và số trừ là $b$. Hiệu là $a-b$. Theo bài ra ta có:
$a+b+(a-b)=2018$

$2\times a=2018$

$a=2018:2=1009$

$a-b=315$

$b=a-315=1009-315=694$ 

Vậy số bị trừ là $1009$ và số trừ là $694$

SBT= 315+ ST

315 + ST+ST + 315

= 315 + 2ST + 315

=2ST+ 630=2018

2ST=2018 -630

2ST=1348

ST= 1348 :2

ST=674

SBT=315+ 674

SBT= 989

Vậy ta có số bị trừ là 989, số trừ là 674.

Các số có thể viết là:427;472;247;274;742;724.

=>Đáp án A là đáp án chính xác.

A.6 số

A. 6 số

Lời giải:
Tổng của 2 số ban đầu:  $24,6+15,4=40$
Khi bớt A đơn vị từ một số và chuyển sang số khác thì tổng không đổi, là $40$ 

Số bé khi đó: $40:(4+1)\times 1=8$ 

Số A là: $15,4-8=7,4$

Cô ơi giải cho em bài 3 và bài 4 em mới gửi với ạ

Bài 1:

1: Thay x=2025 vào A, ta được:

\(A=\dfrac{2025+5}{\sqrt{2025}-2}=\dfrac{2030}{43}\)

2: \(B=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}-\dfrac{4\sqrt{x}}{x-4}\)

\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}-\dfrac{4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)-2\left(\sqrt{x}-2\right)-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)

\(=\dfrac{x+2\sqrt{x}-2\sqrt{x}+4-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)

\(=\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)

3: \(P=A\cdot B=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\cdot\dfrac{x+5}{\sqrt{x}-2}=\dfrac{x+5}{\sqrt{x}+2}\)

\(=\dfrac{x-4+9}{\sqrt{x}+2}=\sqrt{x}-2+\dfrac{9}{\sqrt{x}+2}\)

\(=\sqrt{x}+2+\dfrac{9}{\sqrt{x}+2}-4>=2\cdot\sqrt{\left(\sqrt{x}+2\right)\cdot\dfrac{9}{\sqrt{x}+2}}-4=2\)

Dấu '=' xảy ra khi \(\sqrt{x}+2=\sqrt{9}=3\)

=>x=1(nhận)

Bài 3:

1: Khi m=-2 thì phương trình sẽ trở thành:

\(x^2+2\cdot\left(-2\right)\cdot x-2-3=0\)

=>\(x^2-4x-5=0\)

=>(x-5)(x+1)=0

=>\(\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)

2: \(\text{Δ}=\left(2m\right)^2-4\cdot1\cdot\left(m-3\right)\)

\(=4m^2-4m+12=4m^2-4m+1+11=\left(2m-1\right)^2+11>0\forall m\)

=>Phương trình luôn có 2 nghiệm phân biệt

Theo vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-2m\\x_1x_2=\dfrac{c}{a}=m-3\end{matrix}\right.\)

\(x_1^2+x_1x_2-2x_2^2=3\left(x_1-x_2\right)\)

=>\(x_1^2+2x_1x_2-x_1x_2-2x_2^2=3\left(x_1-x_2\right)\)

=>\(x_1\left(x_1+2x_2\right)-x_2\left(x_1+2x_2\right)-3\left(x_1-x_2\right)=0\)

=>\(\left(x_1-x_2\right)\left(x_1+2x_2-3\right)=0\)

=>\(\left[{}\begin{matrix}x_1=x_2\\x_1+2x_2=3\end{matrix}\right.\)

TH1: \(x_1=x_2\)

mà \(x_1+x_2=-2m\)

nên \(x_1=x_2=-m\)

\(x_1x_2=m-3\)

=>\(\left(-m\right)\cdot\left(-m\right)=m-3\)

=>\(m^2-m+3=0\)

=>\(\left(m-\dfrac{1}{2}\right)^2+\dfrac{11}{4}=0\)(vô lý)

TH2: \(x_1+2x_2=3\)

mà \(x_1+x_2=-2m\)

nên \(x_2=3-\left(-2m\right)=2m+3\)

=>\(x_1=-2m-x_2=-2m-\left(2m+3\right)=-4m-3\)

\(x_1x_2=m-3\)

=>\(\left(2m+3\right)\left(-4m-3\right)=m-3\)

=>\(-8m^2-6m-12m-9=m-3\)

=>\(-8m^2-18m-9-m+3=0\)

=>\(-8m^2-19m-6=0\)

=>\(\left[{}\begin{matrix}m=-\dfrac{3}{8}\\m=-2\end{matrix}\right.\)