Tìm x biết : \(\dfrac{x+4}{2014}\)+\(\dfrac{x+3}{2015}=\dfrac{x+2}{2016}+\dfrac{x+1}{2017}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



câu a :
xét ΔAMB và ΔDMC, ta có :
MB = MC (vì M là trung điểm của BC)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
MA = MD (giả thiết)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
câu b :
\(vì\) \(\Delta AMB=\Delta DMC\) \(nên\) \(\Rightarrow\widehat{ABM}=\widehat{DCM}\) (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong nên => AB // DC
câu a :
xét \(\Delta ADM\) và \(\Delta DMC\), ta có :
\(MB=MC\) (vì M là trung điểm của cạnh BC)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(MA=MD\) (giả thiết)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
câu b :
vì \(\Delta AMB=\Delta DMC\) nên \(\Rightarrow\widehat{ABM}=\widehat{DCM}\) (2 góc tương ứng). Mà 2 góc này ở vị trí soletrong nên AB // DC

\(a,x^2-2=0\Leftrightarrow x^2-\left(\sqrt{2}\right)^2=0\Leftrightarrow\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)
Vậy \(S=\left\{-\sqrt{2};\sqrt{2}\right\}\)
\(b,x\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vậy \(S=\left\{0;2\right\}\)
\(c,x^2-2x=0\Leftrightarrow x\left(x-2\right)\) phương trình như câu b,
\(d,x\left(x^2+1\right)\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=-1\left(voli\right)\end{matrix}\right.\)( voli là vô lí )
Vậy \(S=\left\{0\right\}\)
Tìm 3 số a,b,c biết rằng : a+b+c= 29 , a và b tỉ lệ nghịch với 3 và 2, b và c tỉ lệ thuận với 4 và 3

Lời giải:
Theo bài ra ta có:
$3a=2b; \frac{b}{4}=\frac{c}{3}$
$\Rightarrow \frac{a}{8}=\frac{b}{12}=\frac{c}{9}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{8}=\frac{b}{12}=\frac{c}{9}=\frac{a+b+c}{8+12+9}=\frac{29}{29}=1$
$\Rightarrow a=8.1=8; b=12.1=12; c=9.1=9$

Ta có:
\(\dfrac{x}{10}=\dfrac{y}{5}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}\) \(\left(1\right)\)
\(\dfrac{y}{2}=\dfrac{z}{3}\)
\(\Rightarrow\dfrac{y}{10}=\dfrac{z}{15}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{15}\)
Lại có:
\(\dfrac{z}{15}=\dfrac{4z}{60}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{4z}{60}=\dfrac{x+4z}{20+60}=\dfrac{240}{80}=3\)
\(\Rightarrow x=3\cdot20=60\)
\(y=3\cdot10=30\)
\(z=3\cdot15=45\)

Ta có: ∠BAC + ∠DAC = 180° ( kề bù )
mà ∠BAC = 90° (gt)
⇒ ∠DAC = 180° - 90° = 90°
⇒ ∠BAC = ∠DAC
Xét ∆ABC và ∆ADC có: AB = AC (gt) ; ∠BAC = ∠DAC (cmt) ; AC chung
⇒ ∆ABC = ∆ADC ( c_g_c)
⇒ BC = DC ( 2 cạnh tương ứng )
⇒ ∆CBD cân tại C ( theo dhnb)
Chú thích:
gt: giả thiết
theo dhnb: dấu hiệu nhận biết
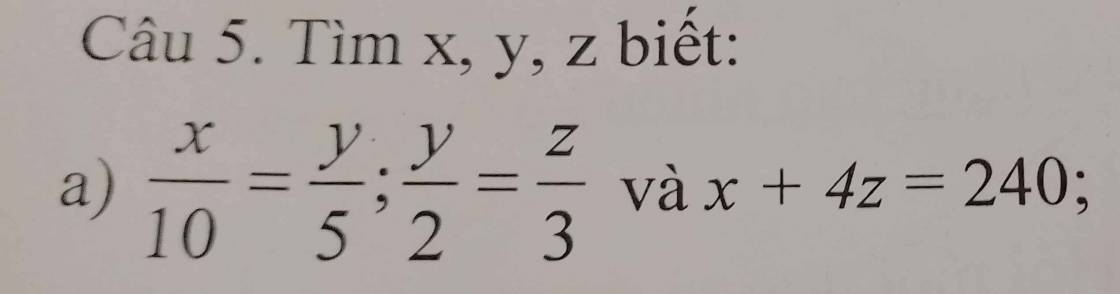
\(\dfrac{x+4}{2014}+\dfrac{x+3}{2015}=\dfrac{x+2}{2016}+\dfrac{x+1}{2017}\)
\(\dfrac{x+4}{2014}+1+\dfrac{x+3}{2015}+1=\dfrac{x+2}{2016}+1+\dfrac{x+1}{2017}+1\)
\(\dfrac{x+2018}{2014}+\dfrac{x+2018}{2015}=\dfrac{x+2018}{2016}+\dfrac{x+2018}{2017}\)
\(\left(x+2018\right)\left(\dfrac{1}{2014}+\dfrac{1}{2015}-\dfrac{1}{2016}-\dfrac{1}{2017}\right)=0\\ x+2018=0\\ x=-2018\)