Hai số có tổng là 5864 .Biết rằng nếu viết thêm chữ số 5 vào bên trái số bé ta được số lớn . Tìm số lớn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Thay m=1 vào (1), ta được:
\(\left\{{}\begin{matrix}x+2y=1+3=4\\2x-3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7y=7\\x+2y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)
b: Vì \(\dfrac{1}{2}\ne\dfrac{2}{-3}\)
nên hệ (1) luôn có nghiệm duy nhất
\(\left\{{}\begin{matrix}x+2y=m+3\\2x-3y=m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=2m+6\\2x-3y=m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y-2x+3y=2m+6-m\\x+2y=m+3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7y=m+6\\x=m+3-2y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{m+6}{7}\\x=m+3-\dfrac{2\left(m+6\right)}{7}=\dfrac{7m+21-2m-12}{7}=\dfrac{5m+9}{7}\end{matrix}\right.\)
x+y=-3
=>\(\dfrac{5m+9+m+6}{7}=-3\)
=>6m+15=-21
=>6m=-36
=>m=-6


Mình tóm tắt thôi nhé, tại bài này cũng khá dài.
a) \(\widehat{AEH}+\widehat{AFH}=90^o+90^o=180^o\) nên tứ giác AEHF nội tiếp
Hơn nữa \(\widehat{ADB}=\widehat{AEB}=90^o\) nên tứ giác AEDB nội tiếp \(\Rightarrow\widehat{DAE}=\widehat{DBE}\) hay \(\widehat{EAH}=\widehat{EBC}\)
b) Dễ chứng minh được: \(\Delta AFH\sim\Delta ADB\Rightarrow AF.AB=AH.AD\)
Mặt khác, \(\widehat{SAF}=\widehat{ACB}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung đó) và \(\widehat{ACB}=\widehat{AFE}\) (\(\Delta AEF\sim\Delta ABC\)) nên \(\widehat{SAF}=\widehat{AFE}\) \(\Rightarrow\) SA//EF. Mà \(SA\perp AO\) nên \(EF\perp AO\).
Do đó, dễ chứng minh rằng \(\Delta AFM\sim\Delta AKB\left(g.g\right)\Rightarrow AF.AB=AM.AK\)
Từ đó suy ra \(AH.AD=AM.AK\Rightarrow\Delta AHM\sim\Delta AKD\)
Lại có tứ giác QDNK nội tiếp ( \(\widehat{QDN}=\widehat{QKN}=90^o\)) nên \(\widehat{AQN}=\widehat{AKD}\) \(\Rightarrow\Delta AKD\sim\Delta AQN\)
Do đó \(\Delta AHM\sim\Delta AQN\) \(\Rightarrow\widehat{AHM}=\widehat{AQN}\) \(\Rightarrow\) QN//HM (2 góc đồng vị bằng nhau)
c) Gọi J là tâm đường tròn (AH)
Dễ chứng minh được \(\Delta FAH\sim\Delta FCB\) \(\Rightarrow\Delta FJA\sim\Delta FIC\)
\(\Rightarrow\widehat{JFA}=\widehat{IFC}\)
Mà \(\widehat{JFA}+\widehat{JFC}=90^o\) nên \(\widehat{IFC}+\widehat{JFC}=90^o\) hay \(\widehat{JFI}=90^o\)
\(\Rightarrow\) IF là tiếp tuyến của (J) tại F.
Tương tự, IE là tiếp tuyến của (J) tại E, do đó \(IJ\perp EF\) Mà EF//SA (cmt) \(\Rightarrow SA\perp IJ\)
Khi đó tam giác ASI có các đường cao AD, IJ cắt nhau tại J nên J là trực tâm tam giác ASI \(\Rightarrow SJ\perp AI\) hay \(SJ\perp AP\)
Lại có \(JA=JP\) nên JS là trung trực của AP \(\Rightarrow SA=SP\) (đpcm)

Giải
Dấu chấm hỏi là 109 nha bạn vì
Ở tam giác 1 ta có
1 mũ 2 + 2 mũ 2 + 3 mũ 2 = 14
Tam giác 2
4 mũ 2 + 5 mũ 2 + 7 mũ 2 = 90
Tam giác 4
4 mũ 2 + 7 mũ 2 + 10 mũ 2 = 165
Từ đó ta có tam giác 3
3 mũ 2 +6 mũ 2 +8 mũ 2 = 109

Vì AB//CD
nên \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}=\dfrac{1}{3}\)
=>\(OC=3OA;OD=3OB\)
Vì OC=3OA
nên \(S_{BOC}=3\times S_{AOB}=3\times6=18\left(cm^2\right)\)
Vì \(OD=3OB\)
nên \(S_{AOD}=3\times S_{AOB}=18\left(cm^2\right)\)
Vì OC=3OA
nên \(S_{DOC}=3\times S_{AOD}=54\left(cm^2\right)\)
\(S_{ABCD}=S_{ABO}+S_{BOC}+S_{DOC}+S_{AOD}\)
\(=6+18+18+54=96\left(cm^2\right)\)

Lời giải:
a.
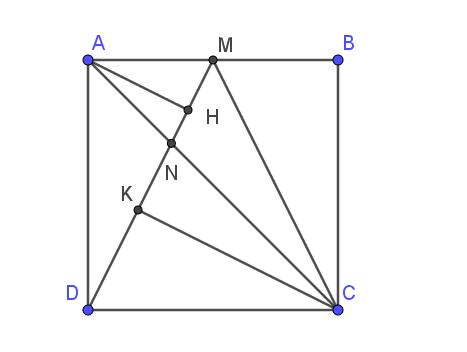
$\frac{S_{DMC}}{S_{DMA}}=\frac{AD\times DC}{2}: \frac{AM\times AD}{2}=\frac{AD\times DC}{AM\times AD}=\frac{DC}{AM}=\frac{AB}{\frac{AB}{2}}=2$
Vậy diện tích tam giác DMC gấp 2 lần diện tích tam giác DMA
b.
Kẻ đường cao AH của tam giác $ADM$ và đường cao $CK$ của tam giác $DCM$
Ta có:
$2=\frac{S_{DCM}}{S_{DMA}}=\frac{CK\times MD}{2}: \frac{AH\times DM}{2}=\frac{CK}{AH}$
Suy ra:
$\frac{S_{ADN}}{S_{DNC}}=\frac{AH\times DN}{2}: \frac{CK\times DN}{2}=\frac{AH}{CK}=\frac{1}{2}$
$2\times S_{ADN}=\times S_{DNC}$
$3\times S_{ADN}=S_{DNC}+S_{ADN}=S_{ADC}=AD\times DC:2=S_{ABCD}:2$
$S_{ABCD}=3\times S_{ADN}\times 2=6\times S_{ADN}=6\times 5=30$ (cm2)

Các tập con của {1; 2; 3; 4; 5} là:
∅; {1}; {2}; {3}; {4}; {5};
{1; 2}; {1; 3}; {1; 4}; {1; 5};
{2; 3}; {2; 4}; {2; 5}
{3; 4}; {3; 5}; {4; 5};
{1; 2; 3}; {1; 2; 4}; {1; 2; 5};
{2; 3; 4}; {2; 3; 5}; {3; 4; 5};
{1; 2; 3; 4}; {1; 2; 3; 5}; {2; 3; 4; 5};
{1; 2; 3; 4; 5}
Các tập con của {1; 2; 3; 4; 5} là:
\(\varnothing\); {1}; {2}; {3}; {4}; {5}; {1; 2}; {1; 3}; {1; 4}; {1; 5}; {2; 3}; {2; 4}; {2; 5};
{3; 4}; {3; 5}; {4; 5}; {1; 2; 3}; {1; 2; 4}; {1; 2; 5}; {1; 3; 4}; {1; 3; 5}; {1; 4; 5}
{2; 3; 4}; {2; 3; 5}; {2; 4; 5}; {3; 4; 5}; {1; 2; 3; 4}; {1; 2; 3; 5}; {1; 2; 4; 5}
{1; 3; 4; 5}; {2; 3; 4; 5}; {1; 2; 3; 4; 5}

Giải thích các bước giải:
Chỉ thiết kế 4 luống hoa chạy suốt theo chiều rộng mảnh vườn
Khi đó chiều dài luống hoa còn là:
40 - 2 x 3 = 34 (m )
Tổng chiều rộng 4 luống hoa còn là:
80 - 5 x 3= 65 (m )
Tổng diện tích 4 luống hoa còn là:
65 x 34= 2210 (m²)
Đap So: 2210 m²


Giúp mình với !
Đây là toán nâng cao tổng hiệu ẩn hiệu, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Vì tổng hai số là số có 4 chữ số đồng thời khi ta viết thêm chữ số 5 vào bên trái số bé ta được số lớn nên số lớn là số có 4 chữ số và hơn số bé 5000 đơn vị
Ta có sơ đồ:
Theo sơ đồ ta có:
Số lớn là: (5864 + 5000) : 2 = 5432
Số bé là: 5432 - 5000 = 432
Đáp số: