Cho a,b,c là ba canhj của tam giác.Chứng minh \(a^2+b^2+c^2\) < 2\(\left(ab+bc+ac\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x+2y=3xy+3\)
\(\Leftrightarrow3xy-x-2y+3=0\)
\(\Leftrightarrow9xy-3x-6y+9=0\)
\(\Leftrightarrow3x\left(3y-1\right)-2\left(3y-1\right)+7=0\)
\(\Leftrightarrow\left(3x-2\right)\left(3y-1\right)=-7\)
| 3x-2 | -7 | -1 | 1 | 7 |
| 3y-1 | 1 | 7 | -7 | -1 |
| x | -5/3(ktm) | 1/3(ktm) | 1 | 3 |
| y | 2/3(ktm) | 8/3(ktm) | -2 | 0 |
Vậy \(\left(x;y\right)=\left(1;-2\right);\left(3;0\right)\)

Ta có: \(f\left(-2\right)=4a-2b+c\)
\(f\left(3\right)=9a+3b+c=13a+b+2c-4a+2b-c=-4a+2b-c\)
\(\Rightarrow f\left(-2\right).f\left(3\right)=\left(4a-2b+c\right)\left(-4a+2b-c\right)=-\left(4a-2b+c\right)^2\le0\) (đpcm)


Câu đánh dấu đỏ của em đây nhé:
\(\dfrac{x}{y}\) = \(\dfrac{2}{3}\) => \(\dfrac{x}{2}\) = \(\dfrac{y}{3}\) => \(\dfrac{x^2}{4}\) = \(\dfrac{x.y}{2.3}\) = \(\dfrac{54}{6}\) = 9
⇒ \(x^2\) = 9.4 = 36 ⇒ \(x^2\) = 62 ⇒ \(x\) = + - 6
\(x\) = 6 ⇒ \(y\) = 6 : \(\dfrac{2}{3}\) = 9;
\(x=-6\) ⇒ \(y=-6\) : \(\dfrac{2}{3}\) = -9

Gọi số tờ tiền mệnh giá 50 000 đồng; 20 000 đồng; 10 000 đồng lần lượt là : x, y, z ( x, y, z \(\in\) N*)
Theo bài ra ta có :
50 000 \(x\) = 20 000 \(y\) = 10 000 \(z\); \(x+y+z=85\)
5\(x\) = 2 \(y\) = \(z\) ⇒ y = \(\dfrac{5}{2}\)\(x\); \(z\) = 5\(x\)
⇒ \(x+\dfrac{5}{2}x+5x\) = 85 ⇒ \(x.(1+\dfrac{5}{2}+5\)) = 85
⇒ \(x\) . \(\dfrac{17}{2}\) = 85 ⇒ \(x\) = 85: \(\dfrac{17}{2}\) ⇒ \(x=10\)
⇒ \(y\) = 10 x \(\dfrac{5}{2}\) = 25; \(z\) = 10.5 = 50
Kêt luận :....

`(2x-15)^5 =(2x-15)^3`
`=>(2x-15)^5 -(2x-15)^3=0`
`=> (2x-15)^3 [(2x-15)^2 -1]=0`
\(\Rightarrow\left[{}\begin{matrix}\left(2x-15\right)^3=0\\\left(2x-15\right)^2-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x-15=0\\\left(2x-15\right)^2=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x-15=0\\2x-15=1\\2x-15=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=15\\2x=16\\2x=14\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{15}{2}\\x=8\\x=7\end{matrix}\right.\)
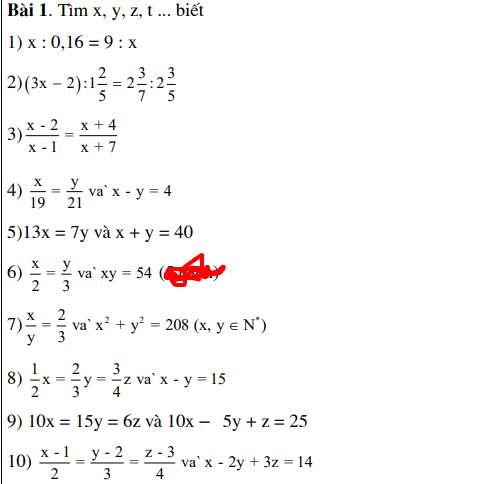
Áp dụng BĐT tam giác:
\(\left\{{}\begin{matrix}a< b+c\\b< a+c\\c< a+b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^2< a\left(b+c\right)\\b^2< b\left(a+c\right)\\c^2< c\left(a+b\right)\end{matrix}\right.\)
Cộng vế:
\(\Rightarrow a^2+b^2+c^2< 2\left(ab+bc+ca\right)\)