Tìm y, biết: \(2\sqrt{9y-27}-\frac{1}{5}\sqrt{25y-75}=10\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : \(\sqrt{x}+1\ge1\forall x\Rightarrow\frac{-4}{\sqrt{x}+1}\ge-4\)
\(\Rightarrow1-\frac{4}{\sqrt{x}+1}\ge1-4=-3\)
Dấu ''='' xảy ra khi x = 0
Vậy GTNN của biểu thức trên bằng -3 tại x = 0

a, \(\sqrt{16\left(x-5\right)}=20\)ĐK : x > = 5
\(\Leftrightarrow4\sqrt{x-5}=20\Leftrightarrow\sqrt{x-5}=5\Leftrightarrow x-5=25\Leftrightarrow x=30\)
b, \(\sqrt{9\left(3-x\right)^2}-12=0\Leftrightarrow3\sqrt{\left(x-3\right)^2}=12\Leftrightarrow\left|x-3\right|=4\)
TH1 : \(x-3=4\Leftrightarrow x=7\)
TH2 : \(x-3=-4\Leftrightarrow x=-1\)
c, tương tự b

Bài 1 :
Xét tam giác MNP vuông tại M, đường cao MH
* Áp dụng hệ thức : \(MH^2=NH.HP\Rightarrow NH=\frac{MH^2}{HP}=\frac{36}{9}=4\)cm
=> NP = HN + HP = 4 + 9 = 13 cm
* Áp dụng hệ thức : \(MN^2=NH.NP=4.13\Rightarrow MN=2\sqrt{13}\)cm
* Áp dụng hệ thức : \(MP^2=PH.NP=9.13\Rightarrow MP=3\sqrt{13}\)cm
Bài 2 :
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AB^2}\Rightarrow\frac{1}{9}=\frac{1}{25}+\frac{1}{AB^2}\Rightarrow AB=\frac{15}{4}\)cm
( bạn nhập biểu thức trên vào máy tính cầm tay rồi shift solve nhé )
* Áp dụng hệ thức : \(AC.AB=AH.BC\Rightarrow BC=\frac{\frac{15}{4}.5}{3}=\frac{25}{4}\)cm





\(x=\sqrt{7}-5\Leftrightarrow x+5=\sqrt{7}\)
\(\Rightarrow\left(x+5\right)^2=7\Leftrightarrow x^2+10x+25=7\)
\(\Leftrightarrow x^2+10x+18=0\)
Vậy đa thức cần tìm có dạng \(f\left(x\right)=a\left(x^2+10x+18\right)\)với \(a\ne0\).
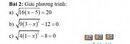

\(2\sqrt{9y-27}-\frac{1}{5}\sqrt{25y-75}=10\)ĐK : y > = 3
\(\Leftrightarrow6\sqrt{y-3}-\sqrt{y-3}=10\Leftrightarrow5\sqrt{y-3}=10\)
\(\Leftrightarrow\sqrt{y-3}=2\Leftrightarrow y-3=4\Leftrightarrow y=7\)