a: Xét tứ giác ABMD có

AD//BM

AB//MD

Do đó: ABMD là hình bình hành

=>AD=BM; AB=MD

Xét tứ giác AEMC có

AE//MC

AC//ME

Do đó: AEMC là hình bình hành

=>AE=MC; ME=AC

Ta có: AE+AD=DE
BM+MC=BC

mà AD=BM và MC=AE

nên DE=BC

Xét ΔABC và ΔMDE có

AB=MD

BC\DE

AC=ME

Do đó: ΔABC=ΔMDE

b: Ta có: AEMC là hình bình hành

=>AM cắt EC tại trung điểm của mỗi đường(1)

Ta có: ABMD là hình bình hành

=>AM cắt BD tại trung điểm của mỗi đường(2)

Từ (1),(2) suy ra AM,EC,BD đồng quy

\(x^3+6x^2+11x+6\)

\(=x^3+x^2+5x^2+5x+6x+6\)

\(=x^2\left(x+1\right)+5x\left(x+1\right)+6\left(x+1\right)\)

\(=\left(x+1\right)\left(x^2+5x+6\right)=\left(x+1\right)\left(x+2\right)\left(x+3\right)\)

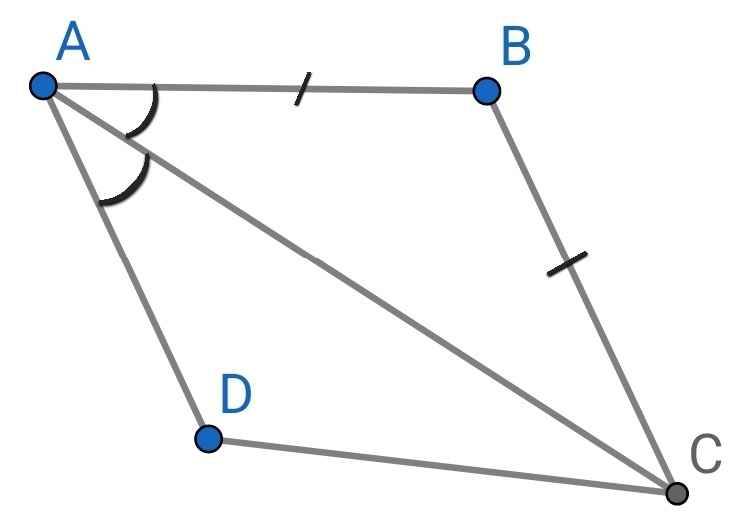
∆ABC có:

AB = BC (gt)

⇒ ∆ABC cân tại B

⇒ ∠BAC = ∠BCA (1)

Do AC là tia phân giác của ∠BAD (gt)

⇒ ∠DAC = ∠BAC (2)

Từ (1) và (2) ⇒ ∠BCA = ∠DAC

Mà ∠BCA và ∠DAC là hai góc so le trong

⇒ BC // AD

⇒ ABCD là hình thang

a) Do x là số nguyên nên 2x + 1 là số nguyên lẻ

Để phân thức đã cho nhận giá trị nguyên thì 2 ⋮ (2x + 1)

⇒ 2x + 1 ∈ Ư(2) = {-1; 1}

⇒ 2x ∈ {-2; 0}

⇒ x ∈ {-1; 0}

Vậy có 2 giá trị nguyên của x thỏa mãn yêu cầu đề bài

b) Ta có:

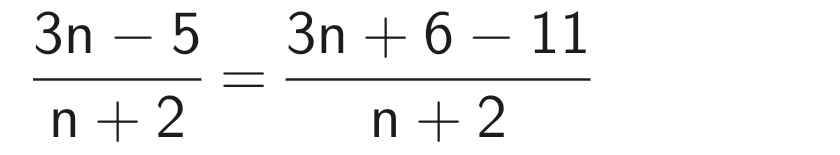
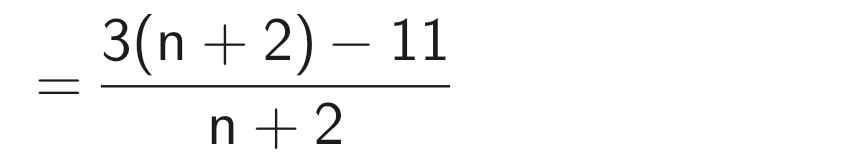
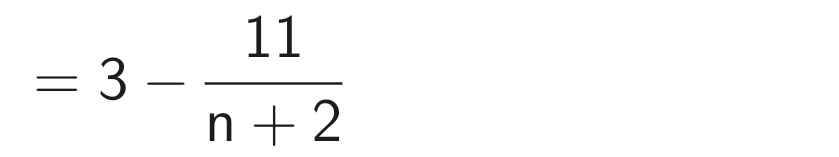
Để phân thức đã cho nhận giá trị nguyên thì 11 ⋮ (n + 2)

⇒ n + 2 ∈ Ư(11) = {-11; -1; 1; 11}

⇒ n ∈ {-13; -3; -1; 9}

Vậy có 4 giá trị nguyên của n thỏa mãn yêu cầu đề bài

|3x - 2| = 4x + 1

|3x - 2| = 3x - 2 khi x ≥ 2/3

|3x - 2| = 2 - 3x khi x < 2/3

*) Với x ≥ 2/3, ta có:

|3x - 2| = 4x + 1

3x - 2 = 4x + 1

3x - 4x = 1 + 2

-x = 3

x = -3 (loại)

*) Với x < 2/3, ta có:

|3x - 2| = 4x + 1

2 - 3x = 4x + 1

-3x - 4x = 1 - 2

-7x = -1

x = 1/7 (nhận)

Vậy phương trình đã cho có 1 nghiệm

Ta có hệ phương trình: a^3 - 3ab^2 = 2,b^3 - 3a^2b = -11
Cộng hai phương trình với nhau ta được:

a^3 - 3ab^2 + b^3 - 3a^2b

= 2 - 11,(a^3 + b^3) - 3ab(a + b)

= -9,(a + b)(a^2 - ab + b^2) - 3ab(a + b)

= -9,(a + b)(a^2 - ab + b^2 - 3ab)

= -9,(a + b)(a^2 - 4ab + b^2) = -9

Ta cần tìm giá trị của a^2 + b^2. Ta có:,(a + b)^2 = a^2 + b^2 + 2ab

Vậy:,a^2 + b^2 = (a + b)^2 - 2ab

Ta có:,a^3 - 3ab^2 = 2,b^3 - 3a^2b = -11
Cộng hai phương trình ta được:

a^3 + b^3 - 3ab(a + b)

= -9,(a + b)(a^2 - ab + b^2) - 3ab(a + b)

= -9,(a + b)(a^2 - ab + b^2 - 3ab)

= -9,(a + b)(a^2 - 4ab + b^2) = -9

Thay a^2 - 4ab + b^2 = -9 vào phương trình (a + b)(a^2 - 4ab + b^2) = -9 ta được:

(a + b)(-9) = -9,a + b = 1
Thay a + b = 1 vào công thức a^2 + b^2 = (a + b)^2 - 2ab

Ta được:,a^2 + b^2 = 1^2 - 2ab,a^2 + b^2 = 1 - 2ab
Vậy để tính a^2 + b^2, chúng ta cần tìm giá trị của ab.
Thay a + b = 1 vào a^3 - 3ab^2 = 2 ta được:

a^3 - 3ab^2 =

2,a^3 - 3a(1 - a)^2

= 2,a^3 - 3a(1 - 2a + a^2)

= 2,a^3 - 3a + 6a^2 - 3a^3

= 2,-2a^3 + 6a^2 - 3a - 2

= 0,2a^3 - 6a^2 + 3a + 2

= 0,2(a^3 - 3a^2 + 3a - 1)

= 0,2(a - 1)^3 = 0
Vậy a = 1 hoặc a = b
Nếu a = 1, ta có:

1 - 3b^2 = 2,-3b^2 = 1,b^2 = -1, không có giá trị thực cho b.
Nếu a = b, ta có:,a^3 - 3a^3 = 2,-2a^3 = 2,a^3 = -1,a = -1
Vậy a = -1, b = -1
Thay a = -1, b = -1 vào a^2 + b^2 = 1 - 2ab ta được:

a^2 + b^2 = 1 - 2(-1)(-1) = 1 - 2 = -1
Vậy kết quả là a^2 + b^2 = -1.

\(A=2\left(x^6+y^6\right)-3\left(x^4+y^4\right)\)

\(=2\left[\left(x^2+y^2\right)^3-3x^2y^2\left(x^2+y^2\right)\right]-3\left[\left(x^2+y^2\right)^2-2x^2y^2\right]\)

\(=2\left[1-3x^2y^2\right]-3\left(1-2x^2y^2\right)\)

\(=2-6x^2y^2-3+6x^2y^2=-1\)

a: Số tiền trả 1 giờ làm theo quy định là:

2000000:40=50000(đồng)

b: Số tiền trả cho 1 giờ làm thêm là:

50000x(1+50%)=75000(đồng)

Tổng số tiền Bình được trả là:

2000000+75000*5=2375000(đồng)