
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: 7-(x-3)=2(3-4x)
=>7-x+3=6-8x
=>-x+10=6-8x
=>-x+8x=6-10
=>7x=-4
=>\(x=-\dfrac{4}{7}\)
2: ĐKXĐ: \(x\notin\left\{1;3\right\}\)
\(\dfrac{3x}{x-1}=\dfrac{2x}{x-3}-\dfrac{4x}{\left(x-1\right)\left(x-3\right)}\)
=>\(\dfrac{3x\left(x-3\right)}{\left(x-1\right)\left(x-3\right)}=\dfrac{2x\left(x-1\right)}{\left(x-3\right)\left(x-1\right)}-\dfrac{4x}{\left(x-1\right)\left(x-3\right)}\)
=>\(3x^2-9x=2x^2-2x-4x\)
=>\(3x^2-9x=2x^2-6x\)
=>\(x^2-3x=0\)
=>x(x-3)=0
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=3\left(loại\right)\end{matrix}\right.\)
3: \(2\left(3x+1\right)-3\left(5x+2\right)>2x-9\)
=>6x+2-15x-6>2x-9
=>-9x-4>2x-9
=>-11x>-5
=>\(x< \dfrac{5}{11}\)

1: |2x-1|=3
=>\(\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2x=4\\2x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(loại\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)
Thay x=-1 vào A, ta được:
\(A=\dfrac{-1-1}{\left(-1\right)^2-4}=\dfrac{-2}{1-4}=\dfrac{-2}{-3}=\dfrac{2}{3}\)
2: \(B=\dfrac{x-3}{x-2}-\dfrac{3}{x+2}-\dfrac{4x+5}{4-x^2}\)
\(=\dfrac{x-3}{x-2}-\dfrac{3}{x+2}+\dfrac{4x+5}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{\left(x-3\right)\left(x+2\right)-3\left(x-2\right)+4x+5}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2-x-6-3x+6+4x+5}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+5}{x^2-4}\)
3: \(\dfrac{A}{B}< 0\)
=>\(\dfrac{x-1}{x^2-4}:\dfrac{x^2+5}{x^2-4}< 0\)
=>\(\dfrac{x-1}{x^2+5}< 0\)
=>x-1<0
=>x<1
Kết hợp ĐKXĐ, ta được:
\(\left\{{}\begin{matrix}x< 1\\x\ne-2\end{matrix}\right.\)


\(A=-\dfrac{2}{5}x^2y.2xy^3\\ =\left(-\dfrac{2}{5}.2\right).\left(x^2.x\right).\left(y.y^3\right)\\ =-\dfrac{4}{5}x^3y^4\)
Hệ số: \(-\dfrac{4}{5}\)
Phần biến: \(x^3y^4\)
Bậc: 3+4=7
A=−52x2y.2xy3=(−52.2).(x2.x).(y.y3)=−54x3y4
Hệ số:
Phần biến:
Bậc: 3+4=7


Đặt 6x+7=a
Phương trình sẽ trở thành \(\left(a+1\right)\left(a-1\right)\cdot a^2=72\)
=>\(a^2\left(a^2-1\right)=72\)
=>\(a^4-a^2-72=0\)
=>\(\left(a^2-9\right)\left(a^2+8\right)=0\)
mà \(a^2+8>0\forall a\)
nên \(a^2-9=0\)
=>(a-3)(a+3)=0
=>(6x+7-3)(6x+7+3)=0
=>(6x+4)(6x+10)=0
=>\(\left[{}\begin{matrix}x=-\dfrac{2}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)
\(\left(6x+8\right)\left(6x+6\right)\left(6x+7\right)^2=72\left(^∗\right)\)
Đặt: \(6x+7=t\)
\(\left(^∗\right)\Rightarrow\left(t+1\right)\left(t-1\right)t^2=72\\ \Leftrightarrow\left(t^2-1\right)t^2=72\\ \Leftrightarrow t^4-t^2-72=0\\ \Leftrightarrow\left(t^4-9t^2\right)+\left(8t^2-72\right)=0\\ \Leftrightarrow t^2\left(t^2-9\right)+8\left(t^2-9\right)=0\\ \Leftrightarrow\left(t^2+8\right)\left(t^2-9\right)=0\\ \Leftrightarrow\left(t^2+8\right)\left(t-3\right)\left(t+3\right)=0\\ \)
\(\Rightarrow\left[{}\begin{matrix}t^2+8=0\left(PTVN\right)\\t-3=0\\t+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=3\\t=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}6x+7=3\\6x+7=-3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)
Vậy pt có tập nghiệm: \(S=\left\{-\dfrac{2}{3};-\dfrac{5}{3}\right\}\)

a: ΔABD vuông tại A
=>\(AB^2+AD^2=BD^2\)
=>\(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
Xét ΔDHA vuông tại H và ΔDAB vuông tại A có
\(\widehat{HDA}\) chung
Do đó: ΔDHA~ΔDAB
=>\(\dfrac{DH}{DA}=\dfrac{AH}{AB}=\dfrac{DA}{DB}\)
=>\(\dfrac{DH}{6}=\dfrac{AH}{8}=\dfrac{6}{10}=\dfrac{3}{5}\)
=>\(DH=6\cdot\dfrac{3}{5}=3,6\left(cm\right);AH=8\cdot\dfrac{3}{5}=4,8\left(cm\right)\)
b: \(\dfrac{DH}{DA}=\dfrac{DA}{DB}\)
=>\(DA^2=DH\cdot DB\)
mà DA=BC
nên \(BC^2=DH\cdot DB\)
c: Xét ΔBME vuông tại M và ΔFMD vuông tại M có
\(\widehat{MBE}=\widehat{MFD}\left(=90^0-\widehat{ADB}\right)\)
Do đó: ΔBME~ΔFMD
e: Xét ΔFDB có
FM,BA là các đường cao
FM cắt BA tại E
Do đó: E là trực tâm của ΔFDB
=>DE\(\perp\)FB
mà DE\(\perp\)KB
và FB,KB có điểm chung là B
nên F,K,B thẳng hàng

a: \(tan\alpha=\dfrac{3}{5}\)
=>\(\dfrac{sin\alpha}{cos\alpha}=\dfrac{3}{5}\)
=>\(sin\alpha=\dfrac{3}{5}cos\alpha\)
\(M=\dfrac{sin\alpha+cos\alpha}{sin\alpha-cos\alpha}=\dfrac{\dfrac{3}{5}cos\alpha+cos\alpha}{\dfrac{3}{5}cos\alpha-cos\alpha}\)
\(=\dfrac{8}{5}:\left(-\dfrac{2}{5}\right)=\dfrac{8}{5}\cdot\dfrac{-5}{2}=-4\)
b: \(N=\dfrac{sin\alpha\cdot cos\alpha}{sin^2\alpha-cos^2\alpha}\)
\(=\dfrac{\dfrac{3}{5}\cdot cos\alpha\cdot cos\alpha}{\left(\dfrac{3}{5}cos\alpha\right)^2-cos^2\alpha}=\dfrac{\dfrac{3}{5}cos^2\alpha}{-\dfrac{16}{25}cos^2\alpha}=\dfrac{3}{5}:\dfrac{-16}{25}\)
\(=\dfrac{3}{5}\cdot\dfrac{-25}{16}=\dfrac{-15}{16}\)
c: \(C=5\cdot cos^2\alpha+2\cdot sin^2\alpha\)
\(=5\cdot\left(1-sin^2\alpha\right)+2\cdot sin^2\alpha\)
\(=5-3\cdot sin^2\alpha=5-3\cdot\left(\dfrac{2}{3}\right)^2=5-3\cdot\dfrac{4}{9}\)
\(=5-\dfrac{4}{3}=\dfrac{11}{3}\)

|2x - 3| = x - 1
Ta có:
|2x - 3| = 2x - 3 khi x ≥ 3/2
|2x - 3| = 3 - 2x khi x < 3/2
*) Với x ≥ 3/2, ta có:
|2x - 3| = x - 1
2x - 3 = x - 1
2x - x = -1 + 3
x = 2 (nhận)
*) Với x < 3/2, ta có:
|2x - 3| = x - 1
3 - 2x = x - 1
-2x - x = -1 - 3
-3x = -4
x = 4/3 (nhận)
Vậy x = 4/3; x = 2

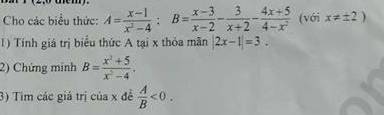


1: Xét ΔEBA vuông tại B và ΔEDF vuông tại D có
\(\widehat{BEA}\) chung
Do đó: ΔEBA~ΔEDF
2: Xét ΔIDA vuông tại D và ΔIBF vuông tại B có
\(\widehat{DIA}=\widehat{BIF}\)(hai góc đối đỉnh)
Do đó: ΔIDA~ΔIBF
=>\(\dfrac{ID}{IB}=\dfrac{IA}{IF}\)
=>\(ID\cdot IF=IA\cdot IB\)