-1/12 - -1/10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(7-\dfrac{1}{5}+\dfrac{1}{3}\right)-\left(6+\dfrac{9}{5}+\dfrac{4}{3}\right)\\ =7-\dfrac{1}{5}+\dfrac{1}{3}-6-\dfrac{9}{5}-\dfrac{4}{3}\\ =\left(7-6\right)-\left(\dfrac{1}{5}+\dfrac{9}{5}\right)+\left(\dfrac{1}{3}-\dfrac{4}{3}\right)\\ =1-2-1\\ =-2\)
\(\left(7-\dfrac{1}{5} +\dfrac{1}{3}\right)-\left(6+\dfrac{9}{5}+\dfrac{4}{3}\right)\)
\(=7-\dfrac{1}{5}+\dfrac{1}{3}-6-\dfrac{9}{5}-\dfrac{4}{3}\)
\(=\left(7-6\right)-\left(\dfrac{1}{5}+\dfrac{9}{5}\right)+\left(\dfrac{1}{3}-\dfrac{4}{3}\right)-\dfrac{1}{3}\)
\(=1-2+\left(-1\right)-\dfrac{1}{3}\)
\(=\left[1+\left(-1\right)\right]-2-\dfrac{1}{3}\)
\(=0-2-\dfrac{1}{3}\)
\(=-2-\dfrac{1}{3}\)
\(=-\dfrac{6}{3}-\dfrac{1}{3}\)
\(=-\dfrac{7}{3}\)

\(\dfrac{4^5.9^4-2.6^9}{2^{10}.3^8+6^8.20}=\dfrac{\left(2^2\right)^5.\left(3^2\right)^4-2.\left(2.3\right)^9}{2^{10}.3^8+\left(2.3\right)^8.\left(2^2.5\right)}\)
\(=\dfrac{2^{10}.3^8-2.2^9.3^9}{2^{10}.3^8+2^8.3^8.2^2.5}=\dfrac{2^{10}.3^8-2^{10}.3^9}{2^{10}.3^8+2^{10}.3^8.5}\)
\(=\dfrac{2^{10}.3^8\left(1-3\right)}{2^{10}.3^8\left(1+5\right)}=\dfrac{-2}{6}=-\dfrac{1}{3}\)
\(\dfrac{4^5\cdot9^4-2\cdot6^9}{2^{10}\cdot3^8+6^8\cdot20}\\ =\dfrac{2^{10}\cdot3^8-2\cdot2^9\cdot3^9}{2^{10}\cdot3^8+2^8\cdot3^8\cdot2^2\cdot5}\\ =\dfrac{2^{10}\cdot3^8-2^{10}\cdot3^9}{2^{10}\cdot3^8+2^{10}\cdot3^8\cdot5}\\ =\dfrac{2^{10}\cdot3^8\cdot\left(1-3\right)}{2^{10}\cdot3^8\cdot\left(1+5\right)}\\ =\dfrac{-2}{6}\\ =-\dfrac{1}{3}\)


\(M=\left(100-1\right)\left(100-2^2\right)\left(100-3^2\right).....\left(100-50^2\right)\\ =\left(100-1\right)\left(100-2^2\right)\left(100-3^2\right).....\left(100-10^2\right).....\left(100-50^2\right)\\ =\left(100-1\right)\left(100-2^2\right)\left(100-3^2\right).....\left(100-100\right).....\left(100-50^2\right)\\ =\left(100-1\right)\left(100-2^2\right)\left(100-3^2\right)....0....\left(100-50^2\right)=0\)

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>DA=DE
b: DA=DE
=>D nằm trên đường trung trực của AE(1)
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra BD là đường trung trực của AE
mà BD cắt AE tại F
nên F là trung điểm của AE
=>CF là đường trung tuyến của ΔAEC

\(\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+.\dfrac{x-64}{9}=10\\ \Leftrightarrow\left(\dfrac{x-85}{15}-1\right)+\left(\dfrac{x-74}{13}-2\right)+\left(\dfrac{x-67}{11}-3\right)+\left(\dfrac{x-64}{9}-4\right)=0\\ \Leftrightarrow\dfrac{x-100}{15}+\dfrac{x-100}{13}+\dfrac{x-100}{11}+\dfrac{x-100}{9}=0\\ \Leftrightarrow\left(x-100\right)\left(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\right)=0\\ \Leftrightarrow x-100=0\\ \Leftrightarrow x=100\)
\(\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}=10\\\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}-10=0\\ \left(\dfrac{x-85}{15}-1\right)+\left(\dfrac{x-74}{13}-2\right)+\left(\dfrac{x-67}{11}-3\right)+\left(\dfrac{x-64}{9}-4\right)=0 \\ \dfrac{x-85-15}{15}+\dfrac{x-74-26}{13}+\dfrac{x-67-33}{11}+\dfrac{x-64-36}{9}=0\\ \dfrac{x-100}{15}+\dfrac{x-100}{13}+\dfrac{x-100}{11}+\dfrac{x-100}{9}=0\\ \left(x-100\right)\cdot\left(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\right)=0\)
Vì \(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\ne0\)

\(A=3^{100}-3^{99}+3^{98}-3^{97}+...+3^2-3+1\\ 3A=3^{101}-3^{100}+3^{99}-3^{98}+...+3^3-3^2+3\\ 3A+A=\left(3^{101}-3^{100}+3^{99}-3^{98}+...+3^3-3^2+3\right)+\left(3^{100}-3^{99}+3^{98}-3^{97}+...+3^2-3+1\right)\\ 4A=3^{101}+\left(3^{100}-3^{100}\right)+\left(3^{99}-3^{99}\right)+...+\left(3^2-3^2\right)+\left(3-3\right)-1\\ 4A=3^{101}-1\\ A=\dfrac{3^{101}-1}{4}\)
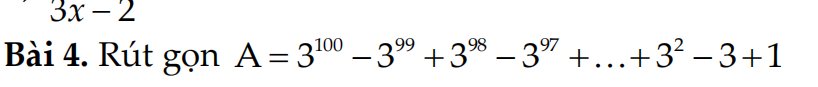
\(-\dfrac{1}{12}-\left(-\dfrac{1}{10}\right)\\ =-\dfrac{1}{12}+\dfrac{1}{10}\\ =\dfrac{-5}{60}+\dfrac{6}{60}\\ =\dfrac{-5+6}{60}\\ =\dfrac{1}{60}\)
-1/12--1/10
=-5/60--6/60
=-11/60