Gọi nửa quãng đường là S

\(t_1\) là thời gian đi hết nửa quãng đường đầu

\(t_1=\dfrac{s}{12}\)

\(t_2\) là thời gian đi hết nửa quãng đường sau

\(t_2=\dfrac{S}{v_2}\)

\(v_{tb}=\dfrac{S+S}{t_1+t_2}=\dfrac{2S}{\dfrac{S}{12}+\dfrac{S}{v_2}}=8\) 

\(\Leftrightarrow\dfrac{2S}{\dfrac{S\left(12+v_2\right)}{12v_2}}=8\Leftrightarrow\dfrac{24v_2}{12+v_2}=8\Rightarrow v_2=6\) km/h

tính x,y,z 

x=3y=27z và 2x-3y+4z=48

 

Vì \(S_1>S_2\Rightarrow R_1< R_2\Rightarrow U_2< U_1 \)

Một con lắc đơn dao động với biên độ góc \(\alpha\) nhỏ. Chu kì con lắc phụ thuộc vào cả chiều dài và vị trí nơi đặt con lắc trên mặt đất.

Khi đó chu kì áp dụng theo công thức: \(T=2\pi\cdot\sqrt{\dfrac{l}{g}}\)

Với chiều dài \(l\) không đổi và tỉ lệ với \(T^2\).

Một con lắc đơn dao đọng với biên độ góc a nhỏ.Chu kì con lắc phụ thuộc vào cả chiều dài và vị trí nơi đặt con lắc trên mặt đất.

Khi đó chu kì áp dụng theo công thức:\(\overline{T+2\pi.\sqrt{\dfrac{l}{g}}}\)

Với chiều dài \(\overline{l}\)không đổi và tỉ lệ với\(^{T^2}\)

\(L=12cm\Rightarrow A=\dfrac{L}{2}=6cm\)

Chu kì dao động: \(T=\dfrac{62,8}{20}=3,14s\approx\pi\left(s\right)\Rightarrow\omega=\dfrac{2\pi}{T}=2\)

Áp dụng pt độc lập: \(x^2+\dfrac{v^2}{\omega^2}=A^2\)

\(\Rightarrow\left(-2\right)^2+\dfrac{v^2}{2^2}=6^2\Rightarrow v=\pm8\sqrt{2}\left(cm/s\right)=\pm0,08\sqrt{2}\left(m/s\right)\)

Mà vật đang chuyển động the chiều dương: \(v=0,08\sqrt{2}\left(m/s\right)\)

Gia tốc vật: 

\(a=-\omega^2x=-2^2\cdot\left(-2\right)=8cm/s^2\)

    

Chu kì \(T=4s\Rightarrow\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{4}=\dfrac{\pi}{2}\)

Trong \(t=6s=T+\dfrac{T}{2}\)

Mà quãng đường đi được sau 6s là 48cm nên:

\(S=4A+2A=6A=48\Rightarrow A=8cm\)

Khi \(t=0\) vật qua VTCB và hướng về vị trí biên âm nên \(\varphi_0=\dfrac{\pi}{2}\).

PT dao động: 

\(x=Acos\left(\omega t+\varphi_0\right)=8cos\left(\dfrac{\pi}{2}t+\dfrac{\pi}{2}\right)\left(cm\right)\)

  

 

 

E = a+1/a-1 = a-1+2/a-1

= 1 +  2/a-1

Để E nguyên => 2/a-1 nguyên

Hay 2 chia hết cho (a-1)

=> a - 1 thuộc Ư(2)={±1;±2}

=> a thuộc { 2;0;3;-1}

\(E=\dfrac{a+1}{a-1}=\dfrac{a-1+2}{a-1}=1+\dfrac{2}{a-1}\)

\(E\in Z\Rightarrow2⋮\left(a-1\right)\)

\(\Rightarrow\left(a-1\right)\inƯ\left(2\right)\)

\(\Rightarrow\left(a-1\right)\in\left\{-1;1;-2;2\right\}\) và \(a\in Z\)

\(\Rightarrow a=\left\{0;2;-1;3\right\}\)

Trung bình (TB) là một khái niệm dùng để chỉ giá trị trung bình của một tập hợp các số hoặc giá trị. Mô (mô-ta) là một đơn vị cấu tạo cơ bản của cơ thể, chẳng hạn như tế bào, mô liên kết, mô cơ, mô thần kinh, vv. Cơ quan là một phần cấu thành của cơ thể, có chức năng cụ thể và thường được hình thành từ nhiều mô khác nhau. Hệ cơ quan là sự kết hợp của các cơ quan có chức năng tương đồng hoặc liên quan nhau, ví dụ như hệ tiêu hóa, hệ tuần hoàn, hệ thần kinh, vv. Cơ thể là tổng thể của tất cả các cơ quan, hệ cơ quan và mô trong cơ thể. Ví dụ minh họa trong thực tế: Hệ tiêu hóa trong cơ thể người. Hệ tiêu hóa bao gồm các cơ quan như dạ dày, ruột non, ruột già, gan, vv. Mỗi cơ quan này được hình thành từ các mô khác nhau như mô cơ, mô liên kết, mô tuyến, vv. Các cơ quan này hoạt động cùng nhau để tiếp nhận, xử lý và hấp thụ thức ăn, đồng thời loại bỏ chất thải. Trung bình (TB) có thể được sử dụng để tính toán lượng thức ăn trung bình mà hệ tiêu hóa cần tiêu thụ hàng ngày để duy trì sức khỏe. ...  

 Từ pt \(v=16\pi\cos\left(4\pi t-\dfrac{\pi}{6}\right)=16\pi\cos\left(4\pi t-\dfrac{2\pi}{3}+\dfrac{\pi}{2}\right)\) (cm/s), ta suy ra \(\omega=4\pi\left(rad/s\right)\), lại có \(\omega A=16\pi\Leftrightarrow A=\dfrac{16\pi}{\omega}=4\left(cm\right)\)

 \(\varphi_0=-\dfrac{2\pi}{3}\); \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)

 Đường tròn lượng giác: 

 

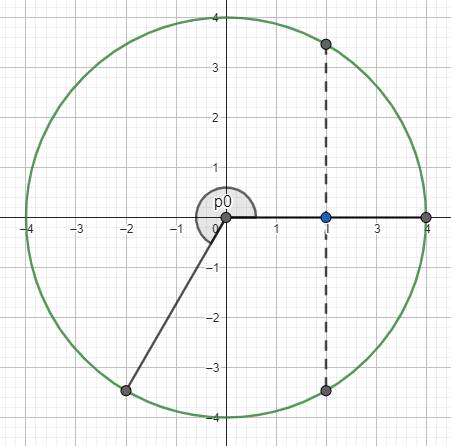
 Từ đây, ta có thể thấy tại thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ khi dao động, góc quét của vật là \(\Delta\varphi=\dfrac{\pi}{3}+1011.2\pi=\dfrac{6067}{3}\pi\) (rad)

 Thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ lúc bắt đầu dao động là \(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{6067}{3}\pi}{2\pi}.0,5=\dfrac{6067}{12}\approx505,58\left(s\right)\)