Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ABCD là hình vuông
=>AB//CD
mà C\(\in\)DE
nên AB//DE
Ta có: DEFG là hình chữ nhật
=>DE//FG
mà AB//DE
nên AB//FG

a: \(\left(x-2\right)\left(3x-1\right)\left(x^2-4x+1\right)\)
\(=\left(3x^2-x-6x+2\right)\left(x^2-4x+1\right)\)
\(=\left(3x^2-7x+2\right)\left(x^2-4x+1\right)\)
\(=3x^4-12x^3+3x^2-7x^3+28x^2-7x+2x^2-8x+2\)
\(=3x^4-19x^3+33x^2-15x+2\)
b: \(x\left(3-4x\right)\left(2x^2-3x\right)\)
\(=\left(-4x^2+3x\right)\left(2x^2-3x\right)\)
\(=-8x^4+12x^3+6x^3-9x^2\)
\(=-8x^4+18x^3-9x^2\)
a)
\(\left(x-2\right)\left(3x-1\right)\left(x^2-4x+1\right)\\ =\left(3x^2-6x-x+2\right)\left(x^2-4x+1\right)\\ =\left(3x^2-7x+2\right)\left(x^2-4x+1\right)\\ =3x^4-12x^3+3x^2-7x^3+28x^2-7x-8x+2\\ =3x^4-19x^3+31x^2-15x+2\)
b)
\(x\left(3-4x\right)\left(2x^2-3x\right)\\ =\left(3x-4x^2\right)\left(2x^2-3x\right)\\ =6x^3-9x^2-8x^4+12x^3\\ =-8x^4+18x^3-9x^2\)

a)
\(32< 2^x< 128\\ =>2^5< 2^x< 2^7\\ =>5< x< 7\\ =>x=6\)
b)
\(2\cdot16\ge2^x>4\\ =>2\cdot2^4\ge2^x>2^2\\ =>2^5\ge2^x>2^2\\ =>5\ge x>2\\ =>x\in\left\{3;4;5\right\}\)
c)
\(9\cdot27\le3^x\le243\\ =>3^2\cdot3^3\le3^x\le3^5\\ =>3^5\le3^x\le3^5\\ =>5\le x\le5\\ =>x=5\)
d)
\(x^{2019}=x\\ =>x^{2019}-x=0\\ =>x\left(x^{2018}-1\right)=0\)
TH1: x = 0
TH2: `x^2018-1=0`
`=>x^2018=1`
`=>x^2018=1^2018`
`=>x=1` hoặc `x=-1`
a: \(32< 2^x< 128\)
=>\(2^5< 2^x< 2^7\)
=>5<x<7
mà x là số tự nhiên
nên x=6
b: \(2\cdot16>=2^x>4\)
=>\(2^5>=2^x>2^2\)
=>2<x<=5
mà x là số tự nhiên
nên \(x\in\left\{3;4;5\right\}\)
c: \(9\cdot27< =3^x< =243\)
=>\(243< =3^x< =243\)
=>\(3^x=243=3^5\)
=>x=5
d: \(x^{2019}=x\)
=>\(x\left(x^{2018}-1\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x^{2018}-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x^{2018}=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
e: \(2^{x+1}+4\cdot2^x=3\cdot2^7\)
=>\(2^x\cdot2+4\cdot2^x=6\cdot2^6\)
=>\(6\cdot2^x=6\cdot2^6\)
=>x=6
f: \(2^{2x}+2^{2x+3}=3^2\cdot8^4\)
=>\(2^{2x}+2^{2x}\cdot8=9\cdot8^4\)
=>\(9\cdot2^{2x}=9\cdot2^{12}\)
=>2x=12
=>x=6
g: \(27^{x+1}=9^{x+5}\)
=>\(3^{3\left(x+1\right)}=3^{2\left(x+5\right)}\)
=>3(x+1)=2(x+5)
=>3x+3=2x+10
=>3x-2x=10-3
=>x=7
h: \(3^{x+2}+5\cdot3^{x+1}=648\)
=>\(3^x\cdot9+5\cdot3^x\cdot3=648\)
=>\(3^x\cdot24=648\)
=>\(3^x=\dfrac{648}{24}=27=3^3\)
=>x=3

a) Thay x=2 vào ta có:
\(2^2-4m\cdot2+1=0\\ \Leftrightarrow4-8m+1=0\\ \Leftrightarrow5-8m=0\\ \Leftrightarrow8m=5\\ \Leftrightarrow m=\dfrac{5}{8}\)
b) Thay x=2 vào ta có:
\(3\cdot2^2-5m\cdot2+7\\ \Leftrightarrow12-10m+7=0\\ \Leftrightarrow19-10m=0\\ \Leftrightarrow10m=19\\\Leftrightarrow m=\dfrac{19}{10}\)
a:
Đặt \(x^2-4mx+1=0\left(1\right)\)
Thay x=2 vào (1), ta được:
\(2^2-4m\cdot2+1=0\)
=>\(4-8m+1=0\)
=>5-8m=0
=>8m=5
=>\(m=\dfrac{5}{8}\)
b: Đặt \(3x^2-5mx+7=0\left(2\right)\)
Thay x=2 vào (2), ta được:
\(3\cdot2^2-5m\cdot2+7=0\)
=>12-10m+7=0
=>19-10m=0
=>10m=19
=>\(m=\dfrac{19}{10}\)

Tỉ số giữa Số học sinh khá và cả lớp là:
\(\dfrac{1}{2}\left(1-\dfrac{1}{4}\right)=\dfrac{1}{2}\cdot\dfrac{3}{4}=\dfrac{3}{8}\)
Số học sinh trung bình chiếm: \(1-\dfrac{3}{8}-\dfrac{1}{4}=\dfrac{5}{8}-\dfrac{2}{8}=\dfrac{3}{8}\)(số học sinh cả lớp)
Số học sinh cả lớp là \(24:\dfrac{3}{8}=24\cdot\dfrac{8}{3}=64\left(bạn\right)\)

\(\left(1:\dfrac{1}{7}\right)^2\left[\left(2^2\right)^3:2^5\right]\cdot\dfrac{1}{49}\\ =7^2\left(2^6:2^5\right)\cdot\dfrac{1}{7^2}\\=\left(7^2\cdot\dfrac{1}{7^2}\right)\cdot2^{6-5}\\ =1\cdot2^1\\ =2\)
\(\left(1:\dfrac{1}{7}\right)^2\left[\left(2^2\right)^3:2^5\right]\cdot\dfrac{1}{49}\)
\(=\dfrac{7^2}{49}\cdot\left(2^6:2^5\right)\)
\(=\dfrac{49}{49}\cdot2=2\)

a)5x+17-(2x+5)=0
=>5x+17-2x-5=0
=>3x+12=0
=>3x=-12
=>x=-12:3=-4
b)3(1-x)-(5-2x)=0
=>3-3x-5+2x=0
=>-2-x=0
=>x=-2
c)2(x-1)-3(x-2)=0
=>2x-2-3x+6=0
=>-x+4=0
=>x=4
d)(x-3)(2x-5)+(2x-4)(5-2x)=0
=>(x-3)(2x-5)-(2x-4)(2x-5)=0
=>(2x-5)(x-3-2x+4)=0
=>(2x-5)(1-x)=0
TH1: 2x - 5=0=>2x=5=>x=5/2
TH2: 1-x=0=>x=1
a: Đặt 5x+17-(2x+5)=0
=>\(5x+17-2x-5=0\)
=>\(3x+12=0\)
=>\(3x=-12\)
=>\(x=-\dfrac{12}{3}=-4\)
b: Đặt \(3\left(1-x\right)-\left(5-2x\right)=0\)
=>\(3-3x-5+2x=0\)
=>\(-x-2=0\)
=>x+2=0
=>x=-2
c: Đặt \(2\left(x-1\right)-3\left(x-2\right)=0\)
=>\(2x-2-3x+6=0\)
=>4-x=0
=>x=4
d: Sửa đề: (x-3)(2x-5)+(2x-4)*(5-x)
Đặt \(\left(x-3\right)\left(2x-5\right)+\left(2x-4\right)\left(5-x\right)=0\)
=>\(2x^2-5x-6x+15+10x-2x^2-20+4x=0\)
=>3x-5=0
=>3x=5
=>\(x=\dfrac{5}{3}\)

Đặt 5x+17-(2x+5)=0
=>5x+17-2x-5=0
=>3x+12=0
=>3x=-12
=>\(x=-\dfrac{12}{3}=-4\)

Diện tích xung quanh của căn phòng là:
\(\left(8+6\right)\times2\times4=8\times14=112\left(m^2\right)\)
Diện tích trần nhà là \(8\times6=48\left(m^2\right)\)
Diện tích cửa ra vào là 1x2,2=2,2(m2)
Diện tích 4 cửa số hình vuông là:
4x0,8x0,8=0,64x4=2,56(m2)
Diện tích cần quét vôi là:
112+48-2,2-2,56=155,24(m2)
Diện tích của tất cả cửa là:
\(1\times2,2+4\times0,8\times0,8=4,76\left(m^2\right)\)
Diện tích xung quanh và trần nhà là::
\(2\times4\times\left(8+6\right)+6\times8=160\left(m^2\right)\)
Diện tich cần quét vôi là:
\(160-4,76=155,24\left(m^2\right)\)
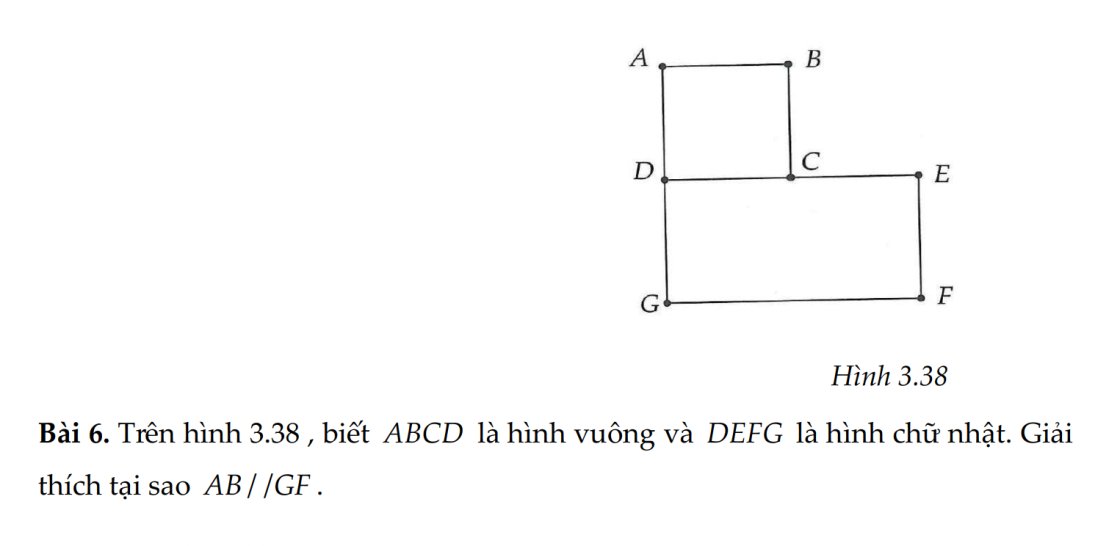
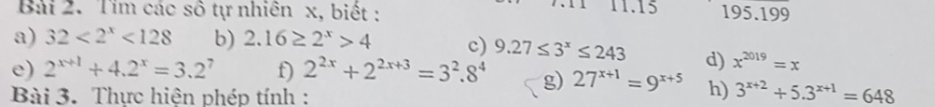
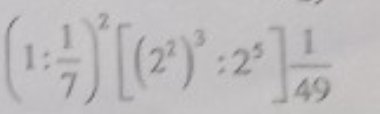
\(A=2^2+2^4+2^6+...+2^{200}\\ 2^2A=2^4+2^6+...+2^{202}\\ 4A-A=\left(2^4+2^6+2^8+...+2^{202}\right)-\left(2^2+2^4+2^6+...+2^{200}\right)\\ 3A=2^{202}-2^2\)
\(=>3A+4=2^{202}-2^2+4=2^{202}-4+4=2^{202}\)
\(=>2^{202}=4^n\\ =>2^{202}=\left(2^2\right)^n\\ =>2^{202}=2^{2n}\\ =>2n=202\\ =>n=101\)