tam giác ABC cân tại A,H là trung điểm của BC
a.Chứng minh tam giác ABH =tam giác AHC và AH vuông góc với BC
b,kẻ HM vuông góc với AC tại M, kẻ HN vuông góc với AC tại N.Chứng minh tam giác AHM=Tam giác AHN
c. Gọi I là giao điểm của MH và AC,K là giao điểm của NH và AB. Chứng minh tam giác AIK là tam giác cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{1}{3}\) - |\(\dfrac{3}{4}\) - \(x\)| = 12
|\(\dfrac{3}{4}\) - \(x\)| = \(\dfrac{1}{3}\) - 12
| \(\dfrac{3}{4}\) - \(x\)| = - \(\dfrac{35}{3}\)
Vì |\(\dfrac{3}{4}\) - \(x\)| ≥ 0 ⇒ - \(\dfrac{35}{3}\) ≥ 0 (vô lý)
Vậy không có giá trị nào của \(x\) thỏa mãn đề bài

a, \(\dfrac{15}{4}\) - 2,5 : |\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3
3,75 - 2,5:|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3
2,5:|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3,75 - 3
2,5 : |\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 0,75
|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 2,5 : 0,75
|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = \(\dfrac{10}{3}\)
\(\left[{}\begin{matrix}\dfrac{3}{4}x+\dfrac{1}{2}=-\dfrac{10}{3}\\\dfrac{3}{4}x+\dfrac{1}{2}=\dfrac{10}{3}\end{matrix}\right.\)
\(\left[{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{10}{3}-\dfrac{1}{2}\\\dfrac{3}{4}x=\dfrac{10}{3}-\dfrac{1}{2}\end{matrix}\right.\)
\(\left[{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{26}{3}\\\dfrac{3}{4}x=\dfrac{17}{6}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-\dfrac{46}{9}\\x=\dfrac{34}{9}\end{matrix}\right.\)

Bài 5:
a, a \(\perp\) m; b \(\perp\) m ⇒ ⇒ a//b (Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
b, \(\widehat{ABb}\) = \(\widehat{aAn}\) = 1300 (hai góc đồng vị)
\(\widehat{Fan}\) = 1800 - 1300 = 500

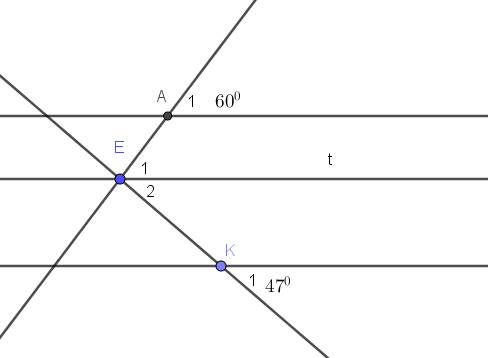
Lời giải:
Kẻ $Et\parallel a\parallel b$. Ta có:
$\widehat{E_1}=\widehat{A_1}=60^0$ (2 góc đồng vị)
$\widehat{E_2}=\widehat{K_1}=47^0$ (2 góc đồng vị)
$\Rightarrow \widehat{AEK}=\widehat{E_1}+\widehat{E_2}=60^0+47^0=107^0$

a, Vì góc dNm và góc HdN ở vị trí so le trong và bằng nhau nên
m//n.
b, \(\widehat{nHt}\) = 1800 - 550 = 1250
\(\widehat{HKN}\) = \(\widehat{nHt}\) = 1250 (hai góc đồng vị)
 bài của cô đúng rồi nhưng cho em hỏi là em làm theo cách này có đúng không nhé
bài của cô đúng rồi nhưng cho em hỏi là em làm theo cách này có đúng không nhé
Vì góc PHK và HKN là 2 góc bù nhau
Suy ra PHK +HKN =180 độ
PHK =180 độ - 55 độ có đúng không ạ nếu sai gì cô góp ý giúp em nhé

52x-3-2.52 =52 . 3
⇔52x-1.52-2.52=52.3
⇔52.(52x-1-2)=52.3
⇔52x-1-2=3
⇔52x-1=5
⇔2x-1=1
⇔2x=2
⇔x=1
vay x=1

a, \(\dfrac{5}{3}\).(- \(\dfrac{6}{5}\) + \(x\)) - \(\dfrac{1}{4}\).(\(\dfrac{2}{3}\) - 1) = - \(\dfrac{3}{8}\)
- 2 + \(\dfrac{5}{3}\)\(x\) - \(\dfrac{1}{6}\) + \(\dfrac{1}{4}\) = - \(\dfrac{3}{8}\)
\(\dfrac{5}{3}\)\(x\) - \(\dfrac{23}{12}\) = -\(\dfrac{3}{8}\)
\(\dfrac{5}{3}\)\(x\) = - \(\dfrac{3}{8}\) + \(\dfrac{23}{12}\)
\(\dfrac{5}{3}\) \(x\) = \(\dfrac{37}{24}\)
\(x\) = \(\dfrac{37}{24}\) : \(\dfrac{5}{3}\)
\(x\) = \(\dfrac{37}{40}\)

Lời giải:
$\frac{5}{3}(-\frac{6}{5}+x)-\frac{1}{4}(\frac{2}{3}-1)=\frac{-3}{8}$
$-2+\frac{5}{3}x+\frac{1}{12}=\frac{-3}{8}$
$\frac{5}{3}x-\frac{23}{12}=\frac{-3}{8}$
$\frac{5}{3}x=\frac{23}{12}+\frac{-3}{8}=\frac{37}{24}$
$x=\frac{37}{24}: \frac{5}{3}=\frac{37}{40}$
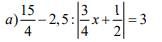 Cíu mình với=(((
Cíu mình với=(((



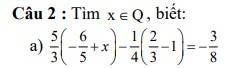
`#3107.101107`
`a,`
Xét $\triangle ABH$ và $\triangle ACH$:
`AB = AC` $(\triangle ABC$cân tại A`)`
\(\widehat{B}=\widehat{C}\) $(\triangle ABC$cân tại A`)`
`HB = HC ( H` là trung điểm của BC`)`
$=> \triangle ABH = \triangle ACH (c - g - c)$
Vì $\triangle ABH = \triangle ACH$
`=>`\(\widehat{AHB}=\widehat{AHC}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí kề bù
`=>` \(\widehat{AHB}+\widehat{AHC}=180^0\)
`=>` \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\) `=> AH \bot BC`
`b,`
Vì $\triangle ABH = \triangle ACH (a)$
`=>`\(\widehat{BAH}=\widehat{CAH}\left(\text{2 góc tương ứng}\right)\)
Xét $\triangle AHM$ và $\triangle AHN$:
AH chung
\(\widehat{MAH}=\widehat{NAH}\left(CMT\right)\)
\(\widehat{AMH}=\widehat{ANH}\left(=90^0\right)\)
$=> \triangle AHM = \triangle AHN (ch - gn)$
`c,`
Xét $\triangle HMB$ và $\triangle HNC$:
\(\widehat{HMB}=\widehat{HNC}\left(=90^0\right)\)
`HB = HC` `(`gt`)`
\(\widehat{HBM}=\widehat{HCN}\) $(\triangle ABC$ cân tại A`)`
$=> \triangle HMB = \triangle HNC (ch - gn)$
`=>`\(\widehat{BHM}=\widehat{CHN}\left(2\text{ góc tương ứng}\right)\) `(1)`
Vì \(\left\{{}\begin{matrix}\widehat{MHB}+\widehat{KHB}=\widehat{MHK}\\\widehat{NHC}+\widehat{IHC}=\widehat{NHI}\end{matrix}\right.\)
Mà \(\widehat{MHK}=\widehat{NHI}\left(\text{đối đỉnh}\right)\) `(2)`
Từ `(1)` và `(2)` `=>` \(\widehat{KHB}=\widehat{IHC}\)
Xét $\triangle KHB$ và $\triangle IHC$:
\(\widehat{KBH}=\widehat{ICH}\left(\widehat{ABC}=\widehat{ACB}\right)\)
`HB = HC`
\(\widehat{KHB}=\widehat{IHC}\)
$=> \triangle KHB = \triangle IHC (g - c - g)$
`=> BK = CI` `(2` cạnh tương ứng`)`
Ta có:
`AK = AB + BK`
`AI = AC + CI`
Mà `AB = AC; BK = CI`
$=> AK = AI => \triangle AIK$ cân tại A.