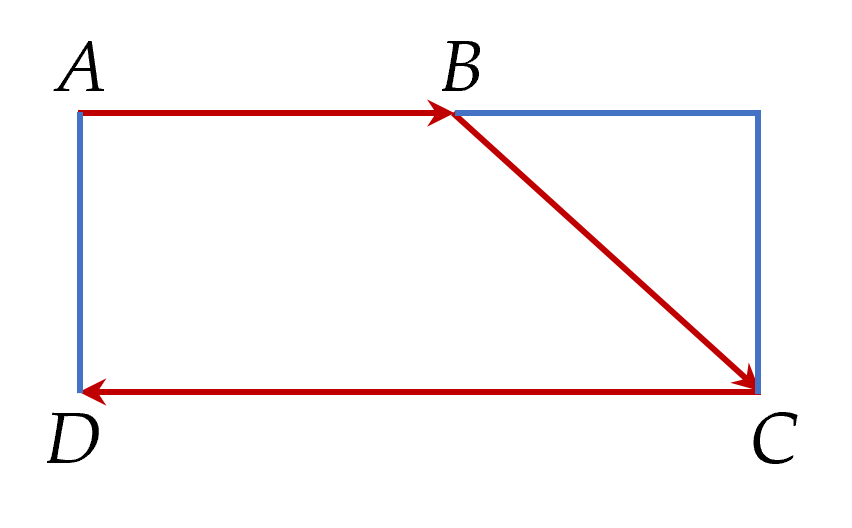
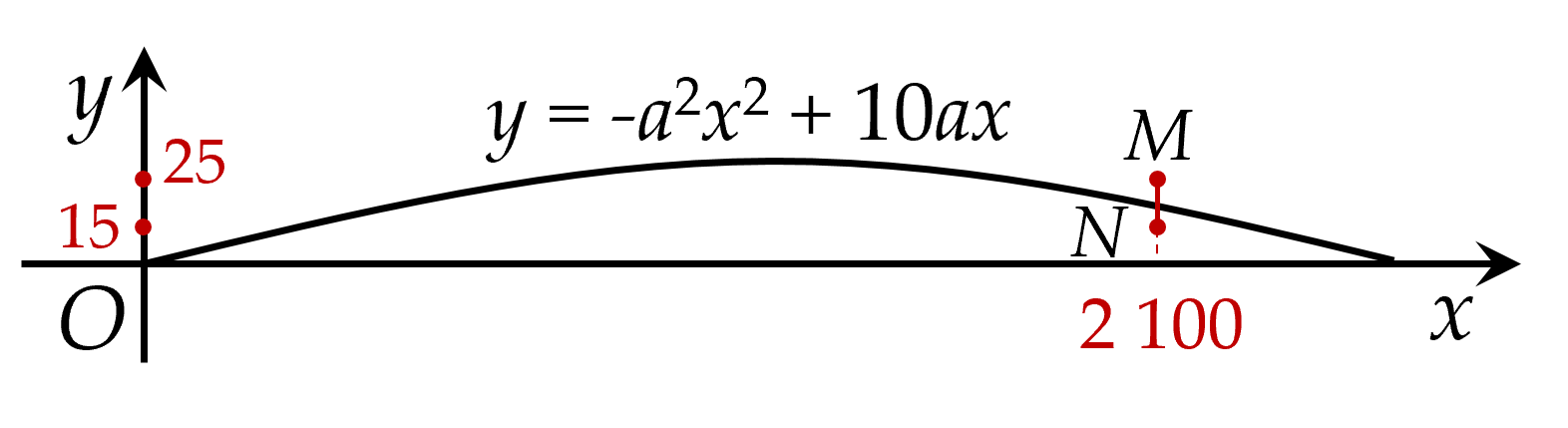Bài 1. Bác Nam dự định trồng ớt và cà trên diện tích $8a$ ($1a=100{{m}^{2}}$). Nếu trồng ớt thì cần $20$ công và thu lãi $3$ $000$ $000$ đồng trên mỗi $a$, nếu trồng cà thì cần $30$ công và thu lãi $4$ $000$ $000$ đồng trên mỗi $a$. Biết tổng số công cần dùng không được vượt quá $180$. Tính số tiền lãi lớn nhất thu được.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}x\ne2m+1\\x\in\left[3;5\right]\end{matrix}\right.\)
=> \(2m+1\notin\left[3;5\right]\)
<=> \(\left\{{}\begin{matrix}2m+1< 3\\2m+1>5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 1\\m>2\end{matrix}\right.\)
=> \(m\in\left(-\infty;1\right)\cup\left(2;+\infty\right)\)

Lời giải:
Gọi $G(a,b)$ là trọng tâm tam giác. Ta có:
$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$
$\Leftrightarrow (1-a, 4-b)+(2-a, -3-b)+(1-a, -2-b)=(0,0)$
$\Leftrightarrow (1-a+2-a+1-a, 4-b-3-b-2-b)=(0,0)$
$\Leftrightarrow (5-3a, -1-3b)=(0,0)$
$\Rightarrow 5-3a=0; -1-3b=0$
$\Rightarrow a=\frac{5}{3}; b=\frac{-1}{3}$
b.
Để $A,B,D$ thẳng hàng thì:
$\overrightarrow{AB}=k\overrightarrow{AD}$ với $k$ là số thực $\neq 0$
$\Leftrightarrow (1,-7)=k(-2, 3m-1)$
$\Leftrightarrow \frac{1}{-2}=\frac{-7}{3m-1}$
$\Rightarrow m=5$

A = {x|xϵ N và x ≤ 7}
A = {0, 1, 2, 3, 4, 5, 6, 7}
B = {x|xϵƯ(21) và x > 0}
B = {1, 3, 7, 21}
=> A ∩ B = {1, 3, 7}

Gọi \(I\) là tâm tỉ cự của 3 điểm A, B, C ứng với bộ \(\left(1,4,1\right)\).
Khi đó: \(\overrightarrow{IA}+4\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\). Gọi Y là trung điểm AC thì \(4\overrightarrow{IB}+2\overrightarrow{IY}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{IY}=-2\overrightarrow{IB}\)
Từ đó dễ dàng xác định được vị trí của I là điểm nằm trên cạnh BY sao cho \(IY=2IB\)
Gọi \(J\) là tâm tỉ cự của 3 điểm A, B, C ứng với bộ \(\left(9,-6,3\right)\). Khi đó \(9\overrightarrow{JA}-6\overrightarrow{JB}+3\overrightarrow{JC}=\overrightarrow{0}\)
\(\Leftrightarrow3\left(\overrightarrow{JA}+\overrightarrow{JC}\right)+6\left(\overrightarrow{JA}-\overrightarrow{JB}\right)=\overrightarrow{0}\)
\(\Leftrightarrow6\overrightarrow{JY}+6\overrightarrow{BA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{JY}=\overrightarrow{AB}\)
Vậy ta thấy J là điểm sao cho tứ giác ABYJ là hình hình hành.

Ta có \(\left|\overrightarrow{MA}+4\overrightarrow{MB}+\overrightarrow{MC}\right|+3\left|3\overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(=\left|\overrightarrow{MI}+\overrightarrow{IA}+4\left(\overrightarrow{MI}+\overrightarrow{IB}\right)+\overrightarrow{MI}+\overrightarrow{IC}\right|+\left|9\left(\overrightarrow{MJ}+\overrightarrow{JA}\right)-6\left(\overrightarrow{MJ}+\overrightarrow{JB}\right)+3\left(\overrightarrow{MJ}+\overrightarrow{JC}\right)\right|\)
\(=\left|6\overrightarrow{MI}\right|+\left|6\overrightarrow{MJ}\right|\)
\(=6\left(MI+MJ\right)\)
Vậy ta cần tìm M để \(MI+MJ\) đạt GTNN. Ta thấy \(MI+MJ\ge IJ=const\). Dấu "=" xảy ra \(\Leftrightarrow\) M nằm trên đoạn thẳng IJ.